вбжЊКЏЪ§fЃЈxЃЉЪЧЖЈвхдк[aЃЌb]ЩЯЕФКЏЪ§ЃЌШєДцдкx
0ЁЪЃЈaЃЌbЃЉЃЌЪЙЕУКЏЪ§дк[aЃЌx
0]ЩЯЕЅЕїЕндіЃЌдк[x
0ЃЌb]ЩЯЕЅЕїЕнМѕЃЌдђГЦy=fЃЈxЃЉЮЊ[aЃЌb]ЩЯЕФЁАЕЅЭЙКЏЪ§ЁБЃЌx
0ГЦЮЊЁАЭЙЕуЁБЃЌАќКЌЁАЭЙЕуЁБЕФЧјМфГЦЮЊЁАКЌЭЙЧјМфЁБЃЎ
ЃЈ1ЃЉХаЖЯЯТСаКЏЪ§жаЃЌФФаЉЪЧ[0ЃЌ1]ЩЯЕФЁАЕЅЭЙКЏЪ§ЁБЃПШєЪЧЃЌжИГіЁАЭЙЕуЁБЃЛШєВЛЪЧЃЌЫЕУїРэгЩЃЎ
Ђйf
1ЃЈxЃЉ=x-2x
2Ђкf
2ЃЈxЃЉ=1-|2x-1|
Ђлf
3ЃЈxЃЉ=|log
2ЃЈx+
ЃЉ|
Ђмf
4ЃЈxЃЉ=sin4x
ЃЈ2ЃЉШєКЏЪ§fЃЈxЃЉ=ax
3+xЃЈaЃМ0ЃЉЪЧ[1ЃЌ2]ЩЯЕФЁАЕЅЭЙКЏЪ§ЁБЃЌЧѓЪЕЪ§aЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉФГбЇЩњбаОПЗЂЯжШчЯТУќЬтЃКЩшy=fЃЈxЃЉЪЧ[aЃЌb]ЩЯЕФЁАЕЅЭЙКЏЪ§ЁБЃЌШєmЃЌnЁЪЃЈaЃЌbЃЉЃЌmЃМnЃЌЧвfЃЈmЃЉЃОfЃЈnЃЉЃЌдђ[aЃЌn]ЮЊy=fЃЈxЃЉЕФЁАКЌЭЙЧјМфЁБЃЌЪдХаЖЯИУУќЬтЕФецМйЃЌВЂЫЕУїРэгЩЃЎ




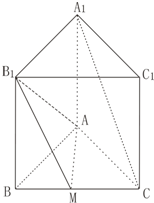 ШчЭМе§Ш§РтжљABC-A1B1C1жаЕзУцБпГЄAB=1ЃЌИпBB1=1ЃЌMЮЊЕзУцBCБпЕФжаЕуЃЎ
ШчЭМе§Ш§РтжљABC-A1B1C1жаЕзУцБпГЄAB=1ЃЌИпBB1=1ЃЌMЮЊЕзУцBCБпЕФжаЕуЃЎ