
定义函数 其导函数记为
其导函数记为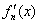 .
.
(1) 求证: ;
;
(2) 设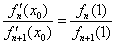 ,求证:
,求证: ;
;
(3) 是否存在区间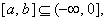 使函数
使函数 在区间
在区间 上的值域为
上的值域为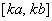 ?
若存在,求出最小的
?
若存在,求出最小的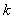 值及相应的区间
值及相应的区间 .
.
(1)∵ ,令
,令
则
当 时
时 ,当
,当 时,
时,
∴ 在
在 上递减,在
上递减,在 上递增
上递增
故 在
在 处取得极(最)小值
处取得极(最)小值
∴ ,即
,即 (当且仅当
(当且仅当 时取等号)……………………4分
时取等号)……………………4分
(2)由 ,得
,得
∴ ,
, ,易知
,易知 ,…………….6分
,…………….6分
而
由(1)知当 时,
时, ,故
,故
∴ ,∴
,∴ …………………………………………………………9分
…………………………………………………………9分
(3)

 令
令 ,得
,得 或
或 ,
,
∴当 时,
时, ;
;
当 时,
时, ;
;
当 时,
时, ,
,
故 的图象如图所示。
的图象如图所示。
下面考查直线 与
与 的相交问题
的相交问题
由图可知直线 与
与 存在交点,
存在交点,
且满足 在区间
在区间 上的值域为
上的值域为
∵在 上,
上, 为图象的极小值点
为图象的极小值点
∴过 作直线
作直线 与
与 的图象交于另一点
的图象交于另一点 ,当直线
,当直线 绕原点
绕原点 顺时钟旋转至点
顺时钟旋转至点 时,满足条件的
时,满足条件的 取最小值,即
取最小值,即 的最小值为
的最小值为 ,相应区间
,相应区间 为
为 。…………………………………………………………………………
。…………………………………………………………………………


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:湖南省2007届高三十校联考第一次考试理科数学试卷 题型:044
定义函数![]() 其导函数记为
其导函数记为![]() .
.
(1)求证:fn(x)≥nx;
(2)设![]() ,求证:0<x0<1;
,求证:0<x0<1;
(3)是否存在区间![]() 使函数h(x)=f3(x)-f2(x)在区间[a,b]上的值域为[ka,kb]?若存在,求出最小的k值及相应的区间[a,b].
使函数h(x)=f3(x)-f2(x)在区间[a,b]上的值域为[ka,kb]?若存在,求出最小的k值及相应的区间[a,b].
查看答案和解析>>
科目:高中数学 来源:2011-2012学年福建省高三第八次月考理科数学试卷 题型:解答题
定义函数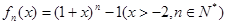 其导函数记为
其导函数记为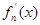 .
.
(Ⅰ)求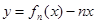 的单调递增区间;
的单调递增区间;
(Ⅱ)若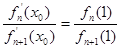 ,求证:
,求证: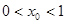 ;
;
(Ⅲ)设函数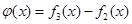 ,数列
,数列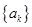 前
前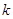 项和为
项和为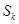 ,
, 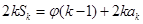 ,其中
,其中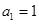 .对于给定的正整数
.对于给定的正整数 ,数列
,数列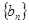 满足
满足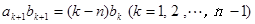 ,且
,且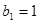 ,求
,求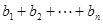 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
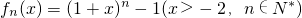 其导函数记为
其导函数记为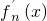 .
.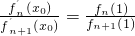 ,求证:0<x0<1;
,求证:0<x0<1;查看答案和解析>>
科目:高中数学 来源:福建省龙岩一中2011-2012学年高三下学期第八次月考试卷数学(理) 题型:解答题
定义函数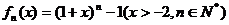 其导函数记为
其导函数记为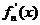 .
.
(Ⅰ)求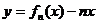 的单调递增区间;
的单调递增区间;
(Ⅱ)若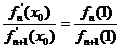 ,求证:
,求证: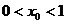 ;
;
(Ⅲ)设函数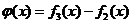 ,数列
,数列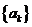 前
前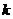 项和为
项和为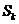 ,
,
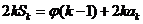 ,其中
,其中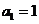 .对于给定的正整数
.对于给定的正整数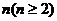 ,数列
,数列 满足
满足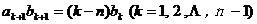 ,且
,且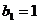 ,求
,求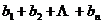 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com