
 ≤
≤
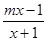 ≥
≥ ,对m进行分类讨论,分别讨论m=0,m>0,m<0的情形,即可得到结果..
,对m进行分类讨论,分别讨论m=0,m>0,m<0的情形,即可得到结果..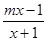 ≥
≥ (1分)
(1分)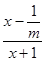 ≥
≥ ,又
,又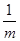 > -1
> -1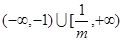 (5分)
(5分)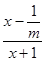 ≤
≤
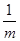 < -1即-1<m<0时,所以原不等式的解集为
< -1即-1<m<0时,所以原不等式的解集为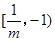
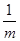 =-1即 m=-1时,所以原不等式的解集为
=-1即 m=-1时,所以原不等式的解集为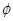
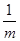 > -1即m<-1时,所以原不等式的解集为
> -1即m<-1时,所以原不等式的解集为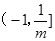 (11分)
(11分)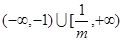
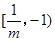
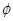


 阅读快车系列答案
阅读快车系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com