
 图象上.
图象上. ,
, 为常数,即证数列{bn}是等比数列.
为常数,即证数列{bn}是等比数列. ,得点
,得点 ,
,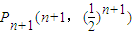 ,从而得斜率
,从而得斜率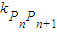 ,即得直线PnPn+1的方程,求得它与x轴,y轴的交点An,Bn,得数列{cn}的通项公式,{cn}的增减性,知
,即得直线PnPn+1的方程,求得它与x轴,y轴的交点An,Bn,得数列{cn}的通项公式,{cn}的增减性,知 ,即得最小的实数t的值.
,即得最小的实数t的值. ,k=8时,和是
,k=8时,和是 ;2008-1120=888是3的倍数,所以存在自然数m,使Sm=2008;求出m的值即可.
;2008-1120=888是3的倍数,所以存在自然数m,使Sm=2008;求出m的值即可. ,
, (常数),
(常数), ,
, ,
, ,
, ,
, ,
, ,
,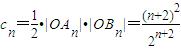 ,
, ,
, ,即最小的实数t的值为
,即最小的实数t的值为 .
. +
+ ,
, ,
, .
.

科目:高中数学 来源: 题型:
| OPn |
| OA |
| OB |
查看答案和解析>>
科目:高中数学 来源: 题型:
| OPn |
| OA |
| OB |
查看答案和解析>>
科目:高中数学 来源: 题型:
A.(3×1006,-4[1-(![]() )1006]) B.(3×1004,-8[1-(
)1006]) B.(3×1004,-8[1-(![]() )1004])
)1004])
C.(3×1002,-4[1-(![]() )1002]) D.(3×1004,-4[1-(
)1002]) D.(3×1004,-4[1-(![]() )1004])
)1004])
查看答案和解析>>
科目:高中数学 来源: 题型:
A.(3×1006,-4[1-(![]() )1006]) B.(3×1004,-8[1-(
)1006]) B.(3×1004,-8[1-(![]() )1004])
)1004])
C.(3×1 002,-4[1-(![]() )1002]) D.(3×1004,-4[1-(
)1002]) D.(3×1004,-4[1-(![]() )1004])
)1004])
查看答案和解析>>
科目:高中数学 来源:2007年广东省深圳市高考数学一模试卷(文科)(解析版) 题型:解答题
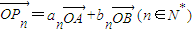 ,其中{an}、{bn}分别为等差数列和等比数列,O为坐标原点,若P1是线段AB的中点.
,其中{an}、{bn}分别为等差数列和等比数列,O为坐标原点,若P1是线段AB的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com