
【题目】已知函数![]() 的图像在点
的图像在点![]() 处的切线方程为
处的切线方程为![]() .
.
(1)求实数![]() 的值及函数
的值及函数![]() 的单调区间;
的单调区间;
(2)当![]() 时,比较
时,比较![]() 与
与![]() (
(![]() 为自然对数的底数)的大小.
为自然对数的底数)的大小.
【答案】(1)函数![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)由![]() 在
在![]() 上得
上得![]() 及
及![]() 得
得![]() 的值,得
的值,得![]() 的解析式,由
的解析式,由![]() 得
得![]() 的增区间,由
的增区间,由![]() 得
得![]() 的减区间;(2)利用函数的单调性结合其图象可知:若
的减区间;(2)利用函数的单调性结合其图象可知:若![]() ,则必有一个小于
,则必有一个小于![]() ,一个大于
,一个大于![]() ,不妨设
,不妨设![]() ,当
,当![]() 时,结论显然成立,当
时,结论显然成立,当![]() 时,
时, ![]() ,令
,令![]() ,对函数求导,可得
,对函数求导,可得![]() 即
即![]() 在
在![]() 单调递增,故
单调递增,故![]() ,得
,得![]() ,结合函数单调性可得结果。
,结合函数单调性可得结果。
(1)函数![]() 的定义域为
的定义域为![]() ,
, ![]() ,
,
因为![]() 的图象在点
的图象在点![]() 处的切线方程为
处的切线方程为![]() ,
,
所以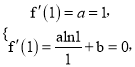 解得
解得![]() ,所以
,所以![]() .
.
所以![]() ,令
,令![]() ,得
,得![]() ,
,
当![]() 时,
时, ![]() ,
, ![]() 单调递增;
单调递增;
当![]() 时,
时, ![]() ,
, ![]() 单调递减.
单调递减.
所以函数![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() .
.
(2)当![]() 时,
时, ![]() .证明如下:
.证明如下:
因为![]() 时,
时, ![]() 单调递减,且
单调递减,且![]() ,
,
又![]() ,当
,当![]() 时,
时, ![]() 单调递增,且
单调递增,且![]() .
.
若![]() ,则
,则![]() 必都大于
必都大于![]() ,且必有一个小于
,且必有一个小于![]() ,一个大于
,一个大于![]() .
.
不妨设![]() ,当
,当![]() 时,必有
时,必有![]() .
.
当![]() 时,
时, ![]() ,
,
设![]() ,
,
则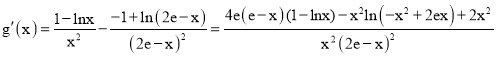
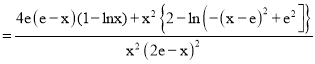
因为![]() ,所以
,所以![]() ,故
,故![]() .
.
又![]() ,所以
,所以![]() ,所以
,所以![]() 在区间
在区间![]() 内单调递增,
内单调递增,
所以![]() ,所以
,所以![]() .
.
因为![]() ,
, ![]() ,所以
,所以![]() ,
,
又因为![]() 在区间
在区间![]() 内单调递增,
内单调递增,
所以![]() ,即
,即![]() .
.
综上,当![]() 时,
时,![]() .
.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案科目:高中数学 来源: 题型:
【题目】某市为了宣传环保知识,举办了一次“环保知识知多少”的问卷调查活动(一人答一份).现从回收的年龄在2060岁的问卷中随机抽取了100份, 统计结果如下面的图表所示.
年龄 分组 | 抽取份 数 | 答对全卷的人数 | 答对全卷的人数占本组的概率 |
[20,30) | 40 | 28 | 0.7 |
[30,40) | n | 27 | 0.9 |
[40,50) | 10 | 4 | b |
[50,60] | 20 | a | 0.1 |
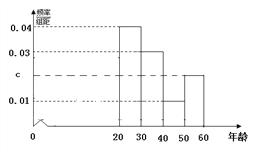
(1)分别求出n, a, b, c的值;
(2)从年龄在[40,60]答对全卷的人中随机抽取2人授予“环保之星”,求年龄在[50,60] 的人中至少有1人被授予“环保之星”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,C、D是以AB为直径的圆上两点,AB=2AD=2 ![]() ,AC=BC,F 是AB上一点,且AF=
,AC=BC,F 是AB上一点,且AF= ![]() AB,将圆沿直径AB折起,使点C在平面ABD的射影E在BD上,已知CE=
AB,将圆沿直径AB折起,使点C在平面ABD的射影E在BD上,已知CE= ![]() .
. 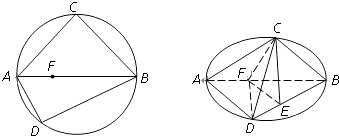
(1)求证:AD⊥平面BCE;
(2)求证:AD∥平面CEF;
(3)求三棱锥A﹣CFD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为椭圆
为椭圆![]() 的左右焦点,点
的左右焦点,点![]() 为其上一点,且有
为其上一点,且有![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,过
两点,过![]() 与
与![]() 平行的直线
平行的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,求四边形
两点,求四边形![]() 的面积
的面积![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知矩形![]() 四点坐标为A(0,-2),C(4,2),B(4,-2),D(0,2).
四点坐标为A(0,-2),C(4,2),B(4,-2),D(0,2).

(1)求对角线![]() 所在直线的方程;
所在直线的方程;
(2)求矩形![]() 外接圆的方程;
外接圆的方程;
(3)若动点![]() 为外接圆上一点,点
为外接圆上一点,点![]() 为定点,问线段PN中点的轨迹是什么,并求出该轨迹方程。
为定点,问线段PN中点的轨迹是什么,并求出该轨迹方程。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设Sn是数列{an}的前n项和. (Ⅰ)若2Sn=3n+3.求{an}的通项公式;
(Ⅱ)若a1=1,an+1﹣an=2n(n∈N*),求Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某房地产开发公司计划在一楼区内建造一个长方形公园ABCD,公园由长方形的休闲区A1B1C1D1(阴影部分)和环公园人行道组成.已知休闲区A1B1C1D1的面积为4000平方米,人行道的宽分别为4米和10米. 
(1)若设休闲区的长A1B1=x米,求公园ABCD所占面积S关于x的函数S(x)的解析式;
(2)要使公园所占面积最小,休闲区A1B1C1D1的长和宽该如何设计?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com