
【题目】如图,在直角梯形![]() 中,
中,![]() .直角梯形
.直角梯形![]() 通过直角梯形
通过直角梯形![]() 以直线
以直线![]() 为轴旋转得到,且使得平面
为轴旋转得到,且使得平面![]() 平面
平面![]() .
.
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)延长![]() 至点
至点![]() ,使
,使![]() 为平面
为平面![]() 内的动点,若直线
内的动点,若直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,且
,且![]() ,求点
,求点![]() 到点
到点![]() 的距离的最小值.
的距离的最小值.

【答案】(1)见解析(2)![]()
【解析】试题分析:(1)由于直角梯形![]() 通过直角梯形
通过直角梯形![]() 以直线
以直线![]() 为轴旋转得到,
为轴旋转得到,![]() ,利用面面垂直的性质可得
,利用面面垂直的性质可得![]() 平面
平面![]() ,进而由面面垂直的判定定理可得结论;(2)由(Ⅰ)可知
,进而由面面垂直的判定定理可得结论;(2)由(Ⅰ)可知![]() 两两垂直.分别以
两两垂直.分别以![]() 为
为![]() 轴、
轴、![]() 轴、
轴、![]() 轴建立空间直角坐标系,
轴建立空间直角坐标系,![]() 的坐标为
的坐标为![]() ,求得
,求得![]() ,利用向量垂直数量积为零求出平面
,利用向量垂直数量积为零求出平面![]() 的一个法向量,利用空间向量夹角余弦公式可得
的一个法向量,利用空间向量夹角余弦公式可得![]() ,进而可得
,进而可得![]() ,进而可得结果.
,进而可得结果.
试题解析:(Ⅰ)![]() 直角梯形
直角梯形![]() 中,
中,![]() ,直角梯形
,直角梯形![]() 通过直角梯形
通过直角梯形![]() 以直线
以直线![]() 为轴旋转得到,
为轴旋转得到,![]() ,又平面
,又平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() 平面
平面![]() .
.
(Ⅱ)由(Ⅰ)可知![]() 两两垂直.分别以
两两垂直.分别以![]() 为
为![]() 轴、
轴、![]() 轴、
轴、![]() 轴建立空间直角坐标系如图所示.由已知
轴建立空间直角坐标系如图所示.由已知![]() ,所以
,所以![]()
![]() ,设
,设![]() 是平面
是平面![]() 的法向量,则
的法向量,则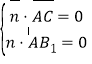 ,即
,即![]() ,取
,取![]() ,得
,得![]() .
.
设![]() 的坐标为
的坐标为![]() ,则
,则![]() ,由
,由![]() ,
,
得![]() ,
,![]() ,
,![]() ,
,
![]() ,所以,
,所以,
当![]() 时,
时,![]() ,
,![]() 点
点![]() 到点
到点![]() 的距离的最小值为
的距离的最小值为![]() .
.


科目:高中数学 来源: 题型:
【题目】某中学在高二年级开设大学先修课程《线性代数》,共有50名同学选修,其中男同学30名,女同学20名.为了对这门课程的教学效果进行评估,学校按性别采用分层抽样的方法抽取5人进行考核.
(Ⅰ)求抽取的5人中男、女同学的人数;
(Ⅱ)考核前,评估小组打算从抽取的5人中随机选出2名同学进行访谈,求选出的两名同学中恰有一名女同学的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中央政府为了应对因人口老龄化而造成的劳动力短缺等问题,拟定出台“延迟退休年龄政策”.为了解人们对“延迟退休年龄政策”的态度,责成人社部进行调研.人社部从网上年龄在15~65岁的人群中随机调查100人,调查数据的频率分布直方图和支持“延迟退休”的人数与年龄的统计结果如下:


(1)由以上统计数据填![]() 列联表,并判断能否在犯错误的概率不超过0.05的前提下认为以45岁为分界点的不同人群对“延迟退休年龄政策”的支持度有差异;
列联表,并判断能否在犯错误的概率不超过0.05的前提下认为以45岁为分界点的不同人群对“延迟退休年龄政策”的支持度有差异;

(2)若以45岁为分界点,从不支持“延迟退休”的人中按分层抽样的方法抽取8人参加某项活动.现从这8人中随机抽2人.
①抽到1人是45岁以下时,求抽到的另一人是45岁以上的概率.
②记抽到45岁以上的人数为![]() ,求随机变量
,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
参考数据:
![]()
![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司招聘员工,先由两位专家面试,若两位专家都同意通过,则视作通过初审予以录用;若两位专家都未同意通过,则视作未通过初审不予录用;当这两位专家意见不一致时,再由第三位专家进行复审,若能通过复审则予以录用,否则不予录用.设应聘人员获得每位初审专家通过的概率为0.5,复审能通过的概率为0.3,各专家评审的结果相互独立.
(Ⅰ)求某应聘人员被录用的概率;
(Ⅱ)若4人应聘,设X为被录用的人数,试求随机变量X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若关于x的不等式e2x﹣alnx![]() a恒成立,则实数a的取值范围是( )
a恒成立,则实数a的取值范围是( )
A.[0,2e]B.(﹣∞,2e]C.[0,2e2]D.(﹣∞,2e2]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着人们经济收入的不断增长,个人购买家庭轿车已不再是一种时尚车的使用费用,尤其是随着使用年限的增多,所支出的费用到底会增长多少,一直是购车一族非常关心的问题某汽车销售公司作了一次抽样调查,并统计得出某款车的使用年限![]() 与所支出的总费用
与所支出的总费用![]() (万元)有如表的数据资料:
(万元)有如表的数据资料:
使用年限 | 2 | 3 | 4 | 5 | 6 |
总费用 | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
(1) 在给出的坐标系中作出散点图;
(2)求线性回归方程![]() 中的
中的![]() 、
、![]() ;
;
(3)估计使用年限为![]() 年时,车的使用总费用是多少?
年时,车的使用总费用是多少?
(最小二乘法求线性回归方程系数公式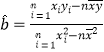 ,
, ![]() .)
.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业欲做一个介绍企业发展史的铭牌,铭牌的截面形状是如图所示的扇形环面(由扇形![]() 挖去扇形
挖去扇形![]() 后构成的).已知
后构成的).已知![]() ,线段
,线段![]() 与弧
与弧![]() 、弧
、弧![]() 的长度之和为
的长度之和为![]() 米,圆心角为
米,圆心角为![]() 弧度.
弧度.

(1)求![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(2)记铭牌的截面面积为![]() ,试问
,试问![]() 取何值时,
取何值时,![]() 的值最大?并求出最大值.
的值最大?并求出最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,过
,过![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,
两点,![]() 的周长为
的周长为![]() .
.
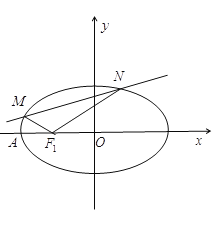
(1)求椭圆![]() 的方程;
的方程;
(2)如图,点![]() ,
,![]() 分别是椭圆
分别是椭圆![]() 的左顶点、左焦点,直线
的左顶点、左焦点,直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() 、
、![]() (
(![]() 、
、![]() 都在
都在![]() 轴上方).且
轴上方).且![]() .证明:直线
.证明:直线![]() 过定点,并求出该定点的坐标.
过定点,并求出该定点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com