练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，在平面四边形ABCD中，已知A＝，B＝，AB＝6.在AB边上取点E，使得BE＝1，连接EC，ED.若∠CED＝，EC＝.

    (1)求sin∠BCE的值；

    (2)求CD的长.

    【答案】(1) (2)7

    【解析】

    （1）在三角形中，利用正弦定理求得.

    （2）证得，结合（1）中的值，求得的值，在直角三角形中求得的值，在三角形中，利用余弦定理求得.

    (1)在△BEC中，由正弦定理，知＝，

    因为B＝，BE＝1，CE＝，

    所以sin∠BCE＝＝＝.

    (2)因为∠CED＝B＝，所以∠DEA＝∠BCE，

    所以cos∠DEA＝＝＝＝.

    因为，所以△AED为直角三角形，又AE＝5，

    所以ED＝＝＝2.

    在△CED中，CD2＝CE2＋DE2－2CE·DE·cos∠CED＝7＋28－2××2×＝49.

    所以CD＝7.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知抛物线的焦点和，点为抛物线上的动点，则取到最小值时点的坐标为（ ）

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数，，其中.

    （1）若，，求函数在处的切线方程；

    （2）讨论的单调区间.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知某几何体的直观图和三视图如下图所示，其正视图为矩形，侧视图为等腰直角三角形，俯视图为直角梯形.

    （1）为中点，在线段上是否存在一点，使得平面？若存在，求出的长；若不存在，请说明理由；

    （2）求二面角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知向量， ，设函数，且的图象过点和点.

    （Ⅰ）求的值；

    （Ⅱ）将的图象向左平移（）个单位后得到函数的图象.若的图象上各最高点到点的距离的最小值为1，求的单调增区间.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，曲线在点处的切线与直线垂直（其中为自然对数的底数）．

    （I）求的解析式及单调递减区间；

    （II）若存在 ，使函数成立，求实数的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某地举办科技博览会，有个场馆，现将个志愿者名额分配给这个场馆，要求每个场馆至少有一个名额且各场馆名额互不相同的分配方法共有（ ）种

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知，两点，满足:，，，则的最大值为________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

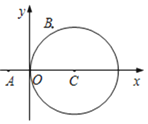
    【题目】如图，在平面直角坐标系xOy中，已知圆C：x2+y2-4x=0及点A（-1，0），B（1，2）

    （1）若直线l平行于AB，与圆C相交于M，N两点，MN=AB，求直线l的方程；

    （2）若圆C上存在两个点P，使得PA2+PB2=a（a＞4），求a的取值范围．

    查看答案和解析>>

    同步练习册答案