解:(I)f'(x)=x
2-a,g'(x)=2bx.
因为曲线y=f(x)与曲线y=g(x)在它们的交点(1,c)处具有公共切线,
所以f(1)=g(1),且f'(1)=g'(1),即

,且1-a=2b,
解得

.
(II)记h(x)=f(x)+g(x),
当a=1-2b时,

,h'(x)=x
2+(1-a)x-a=(x+1)(x-a),
令h'(x)=0,得x
1=-1,x
2=a>0.
当x变化时,h'(x),h(x)的变化情况如下表:
| x | (-∞,-1) | -1 | (-1,a) | a | (a,+∞) |
| h'(x) | + | 0 | - | 0 | + |
| h(x) | ↗ | 极大值 | ↘ | 极小值 | ↗ |
所以函数h(x)的单调递增区间为(-∞,-1),(a,+∞);单调递减区间为(-1,a),
故h(x)在区间(-2,-1)内单调递增,在区间(-1,0)内单调递减,
从而函数h(x)在区间(-2,0)内恰有两个零点,当且仅当
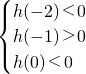
,解得

,
所以a的取值范围是
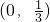
.
(III)记h(x)=f(x)+g(x),当a=1-2b=1时,
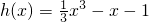
.
由(II)可知,函数h(x)的单调递增区间为(-∞,-1),(1,+∞);单调递减区间为(-1,1).
①当t+3<-1时,即t<-4时,h(x)在区间[t,t+3]上单调递增,
所以h(x)在区间[t,t+3]上的最大值为
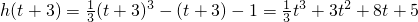
;
②当t<-1且-1≤t+3<1,即-4≤t<-2时,h(x)在区间[t,-1)上单调递增,在区间[-1,t+3]上单调递减,
所以h(x)在区间[t,t+3]上的最大值为
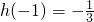
;
当t<-1且t+3≥1,即-2≤t<-1时,t+3<2且h(2)=h(-1)=-

,
所以h(x)在区间[t,t+3]上的最大值为
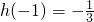
;
③当-1≤t<1时,t+3≥2>1,h(x)在区间[t,1)上单调递减,在区间[1,t+3]上单调递增,
而最大值为h(t)与h(t+3)中的较大者.
由h(t+3)-h(t)=3(t+1)(t+2)知,当-1≤t<1时,h(t+3)≥h(t),
所以h(x)在区间[t,t+3]上的最大值为

;
④当t≥1时,h(x)在区间[t,t+3]上单调递增,
所以h(x)在区间[t,t+3]上的最大值为

.
分析:(I)求出f'(x),g'(x),由题意得f(1)=g(1),且f'(1)=g'(1),解该方程组即可;
(II)记h(x)=f(x)+g(x),当a=1-2b时,

,利用导数可研究其单调性、极值情况,由函数在(-2,0)内有两零点可得端点处函数值及极值符号,由此得一不等式组,解出即可;
(III)当a=1-2b=1时,
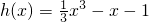
.由(II)可知,函数h(x)的单调区间及极值点,按照在区间[t,t+3]内没有极值点,一个极值点,两个极值点分类讨论,结合图象及函数的单调性即可求得其最大值;
点评:本题考查利用导数研究曲线上某点切线方程、函数的零点及函数在闭区间上的最值问题,考查分类讨论思想、数形结合思想,考查学生综合运用知识分析解决问题的能力,综合性强,难度大.

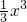 -ax(a>0),g(x)=bx2+2b-1.
-ax(a>0),g(x)=bx2+2b-1. ,且1-a=2b,
,且1-a=2b, .
. ,h'(x)=x2+(1-a)x-a=(x+1)(x-a),
,h'(x)=x2+(1-a)x-a=(x+1)(x-a),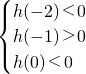 ,解得
,解得 ,
,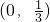 .
.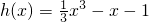 .
.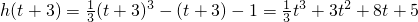 ;
;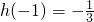 ;
; ,
,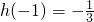 ;
; ;
; .
. ,利用导数可研究其单调性、极值情况,由函数在(-2,0)内有两零点可得端点处函数值及极值符号,由此得一不等式组,解出即可;
,利用导数可研究其单调性、极值情况,由函数在(-2,0)内有两零点可得端点处函数值及极值符号,由此得一不等式组,解出即可;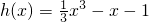 .由(II)可知,函数h(x)的单调区间及极值点,按照在区间[t,t+3]内没有极值点,一个极值点,两个极值点分类讨论,结合图象及函数的单调性即可求得其最大值;
.由(II)可知,函数h(x)的单调区间及极值点,按照在区间[t,t+3]内没有极值点,一个极值点,两个极值点分类讨论,结合图象及函数的单调性即可求得其最大值;

 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案