
设函数y=f(x)对任意实数x,都有f(x)=2f(x+1),当x∈[0,1]时,f(x)=![]() x2(1-x).
x2(1-x).
(Ⅰ)已知n∈N+,当x∈[n,n+1]时,求y=f(x)的解析式;
(Ⅱ)求证:对于任意的n∈N+,当x∈[n,n+1]时,都有|f(x)|≤![]() ;
;
(Ⅲ)对于函数y=f(x)(x∈[0,+∞![]() ,若在它的图象上存在点P,使经过点P的切线与直线x+y=1平行,那么这样点有多少个?并说明理由.
,若在它的图象上存在点P,使经过点P的切线与直线x+y=1平行,那么这样点有多少个?并说明理由.
解:(Ⅰ)由f(x)=2f(x+1)→f(x)=![]() (x-1),x∈[n,n+1],则(x-n)∈[0,1]
(x-1),x∈[n,n+1],则(x-n)∈[0,1]
→f(x-n)=![]() (x-n)2(1+n-x). f(x)=
(x-n)2(1+n-x). f(x)=![]() f(x-1)=
f(x-1)=![]() f(x-2)=…=
f(x-2)=…=![]() f(x-n)=
f(x-n)=![]() (x-n)2(1+n-x). (n=0也适用). ………………4分
(x-n)2(1+n-x). (n=0也适用). ………………4分
(Ⅱ)f![]() (x)=
(x)=![]() ,由f
,由f![]() (x)=0得x=n或x=n+
(x)=0得x=n或x=n+![]()
| x | n | (n,n+ | n+ | (n+ | n+1 |
| f | + | 0 | - | + | |
| 0 | ↗ | 极大 | ↘ | 0 |
f(x)的极大值为f(x)的最大值,![]() ,
,
又f(x)≥f(n)=f(n+1)=0,∴|f(x)|=f(x)≤![]() (x∈[n,n+1]).…8分
(x∈[n,n+1]).…8分
(Ⅲ)y=f(x),x∈[0,+∞![]() 即为y=f(x),x∈[n,n+1],f
即为y=f(x),x∈[n,n+1],f![]() (x)=-1.
(x)=-1.
本题转化为方程f![]() (x)=-1在[n,n+1]上有解问题
(x)=-1在[n,n+1]上有解问题
即方程![]() 在[n,n+1]内是否有解. ……11分
在[n,n+1]内是否有解. ……11分
令g(x)=![]() ,
,
对轴称x=n+![]() ∈[n,n+1],
∈[n,n+1],
又△=…=![]() ,g(n)=
,g(n)=![]() ,g(n+1)=
,g(n+1)=![]() ,
,
①当0≤n≤2时,g(n+1)≥0,∴方程g(x)=0在区间[0,1],[1,2],[2,3]上分别有一解,即存在三个点P;
②n≥3时,g(n+1)<0,方程g(x)=0在[n,n+1]上无解,即不存在这样点P.
综上所述:满足条件的点P有三个. …………………………16分


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:
| 2x | ||
2x+
|
| op |
| 1 |
| 2 |
| op1 |
| op2 |
| 1 |
| 2 |
| 1 |
| n |
| 2 |
| n |
| n-1 |
| n |
| n |
| n |
| 1 | ||||
(Sn+
|
| 2 |
查看答案和解析>>
科目:高中数学 来源:2012届江苏省泰州中学高三上学期期中考试数学 题型:解答题
(本题满分16分)设函数y=f(x)对任意实数x,都有f(x)=2f(x+1),当x∈[0,1]时,f(x)=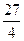 x2(1-x).
x2(1-x).
(Ⅰ)已知n∈N+,当x∈[n,n+1]时,求y=f(x)的解析式;
(Ⅱ)求证:对于任意的n∈N+,当x∈[n,n+1]时,都有|f(x)|≤ ;
;
(Ⅲ)对于函数y=f(x) (x∈[0,+∞
(x∈[0,+∞ ,若在它的图象上存在点P,使经过点P的切线与直线x+y=1平行,那么这样点有多少个?并说明理由
,若在它的图象上存在点P,使经过点P的切线与直线x+y=1平行,那么这样点有多少个?并说明理由
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江苏省高三上学期期中考试数学 题型:解答题
(本题满分16分)设函数y=f(x)对任意实数x,都有f(x)=2f(x+1),当x∈[0,1]时,f(x)= x2(1-x).
x2(1-x).
(Ⅰ)已知n∈N+,当x∈[n,n+1]时,求y=f(x)的解析式;
(Ⅱ)求证:对于任意的n∈N+,当x∈[n,n+1]时,都有|f(x)|≤ ;
;
(Ⅲ)对于函数y=f(x)(x∈[0,+∞ ,若在它的图象上存在点P,使经过点P的切线与直线x+y=1平行,那么这样点有多少个?并说明理由
,若在它的图象上存在点P,使经过点P的切线与直线x+y=1平行,那么这样点有多少个?并说明理由
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com