
【题目】已知函数![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)若函数![]() 在
在![]() 有两个零点,求m的取值范围.
有两个零点,求m的取值范围.
【答案】(1)答案不唯一,具体见解析(2)![]()
【解析】
(1)首先求出函数的导函数因式分解为![]() ,再对参数
,再对参数![]() 分类讨论可得;
分类讨论可得;
(2)依题意可得![]() ,当
,当![]() 函数在定义域上单调递增,不满足条件;
函数在定义域上单调递增,不满足条件;
当![]() 时,由(1)得
时,由(1)得![]() 在
在![]() 为增函数,因为
为增函数,因为![]() ,
,![]() .再对
.再对![]() ,
,![]() ,
,![]() 三种情况讨论可得.
三种情况讨论可得.
解:(1)因为![]() ,所以
,所以![]() ,
,
即![]() .
.
由![]() ,得
,得![]() ,
,![]() .
.
①当![]() 时,
时,![]() ,当且仅当
,当且仅当![]() 时,等号成立.
时,等号成立.
故![]() 在
在![]() 为增函数.
为增函数.
②当![]() 时,
时,![]() ,
,
由![]() 得
得![]() 或
或![]() ,由
,由![]() 得
得![]() ;
;
所以![]() 在
在![]() ,
,![]() 为增函数,在
为增函数,在![]() 为减函数.
为减函数.
③当![]() 时,
时,![]() ,
,
由![]() 得
得![]() 或
或![]() ,由
,由![]() 得
得![]() ;
;
所以![]() 在
在![]() ,
,![]() 为增函数,在
为增函数,在![]() 为减函数.
为减函数.
综上,当![]() 时,
时,![]() 在为
在为![]() 增函数;
增函数;
当![]() 时,
时,![]() 在
在![]() ,
,![]() 为增函数,在
为增函数,在![]() 为减函数;
为减函数;
当![]() 时,
时,![]() 在
在![]() ,
,![]() 为增函数,在
为增函数,在![]() 为减函数.
为减函数.
(2)因为![]() ,所以
,所以![]() ,
,
①当![]() 时,
时,![]() ,
,![]() 在
在![]() 为增函数,所以
为增函数,所以![]() 在
在![]() 至多一个零点.
至多一个零点.
②当![]() 时,由(1)得
时,由(1)得![]() 在
在![]() 为增函数.
为增函数.
因为![]() ,
,![]() .
.
(ⅰ)当![]() 时,
时,![]() ,
,![]() 时,
时,![]() ,
,![]() 时,
时,![]() ;
;
所以![]() 在
在![]() 为减函数,在
为减函数,在![]() 为增函数,
为增函数,![]() .
.
故![]() 在
在![]() 有且只有一个零点.
有且只有一个零点.
(ⅱ)当![]() 时,
时,![]() ,
,![]() ,
,![]() ,使得
,使得![]() ,
,
且![]() 在
在![]() 为减函数,在
为减函数,在![]() 为增函数.
为增函数.
所以![]() ,又
,又![]() ,
,
根据零点存在性定理,![]() 在
在![]() 有且只有一个零点.
有且只有一个零点.
又![]() 在
在![]() 上有且只有一个零点0.
上有且只有一个零点0.
故当![]() 时,
时,![]() 在
在![]() 有两个零点.
有两个零点.
(ⅲ)当![]() 时,
时,![]() ,
,![]() ,
,![]() ,使得
,使得![]() ,
,
且![]() 在
在![]() 为减函数,在
为减函数,在![]() 为增函数.
为增函数.
因为![]() 在
在![]() 有且只有一个零点0,
有且只有一个零点0,
若![]() 在
在![]() 有两个零点,则
有两个零点,则![]() 在
在![]() 有且只有一个零点.
有且只有一个零点.
又![]() ,所以
,所以![]() 即
即![]() ,所以
,所以![]() ,
,
即当![]() 时
时![]() 在
在![]() 有两个零点.
有两个零点.
综上,m的取值范围为![]()


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xoy中,以坐标原点O为极点,x轴正半轴为极轴建立极坐标系。已知曲线C的极坐标方程为![]() ,过点
,过点![]() 的直线l的参数方程为
的直线l的参数方程为 (为参数),直线l与曲线C交于M、N两点。
(为参数),直线l与曲线C交于M、N两点。
(1)写出直线l的普通方程和曲线C的直角坐标方程:
(2)若![]() 成等比数列,求a的值。
成等比数列,求a的值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某地某月1日至15日的日平均温度变化的折线图,根据该折线图,下列结论正确的是( )
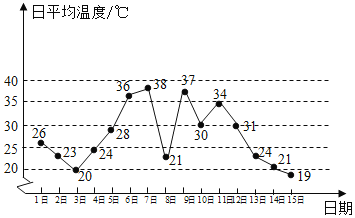
A. 这15天日平均温度的极差为![]()
B. 连续三天日平均温度的方差最大的是7日,8日,9日三天
C. 由折线图能预测16日温度要低于![]()
D. 由折线图能预测本月温度小于![]() 的天数少于温度大于
的天数少于温度大于![]() 的天数
的天数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】依照某发展中国家2018年的官方资料,将该国所有家庭按年收入从低到高的顺序平均分为五组,依次为第一组至第五组,各组家庭的年收入总和占该国全部家庭的年收入总和的百分比如图所示.
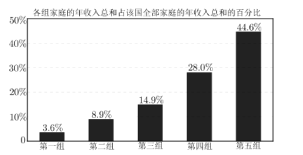
以下关于该国2018年家庭收入的判断,一定正确的是( )
A. 至少有![]() 的家庭的年收入都低于全部家庭的平均年收入
的家庭的年收入都低于全部家庭的平均年收入
B. 收入最低的那![]() 的家庭平均年收入为全部家庭平均年收入的
的家庭平均年收入为全部家庭平均年收入的![]()
C. 收入最高的那![]() 的家庭年收入总和超过全部家庭年收入总和的
的家庭年收入总和超过全部家庭年收入总和的![]()
D. 收入最低的那![]() 的家庭年收入总和超过全部家庭年收入总和的
的家庭年收入总和超过全部家庭年收入总和的![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定点![]() ,
,![]() ,直线
,直线![]() 、
、![]() 相交于点
相交于点![]() ,且它们的斜率之积为
,且它们的斜率之积为![]() ,记动点
,记动点![]() 的轨迹为曲线
的轨迹为曲线![]() 。
。
(1)求曲线![]() 的方程;
的方程;
(2)过点![]() 的直线与曲线
的直线与曲线![]() 交于
交于![]() 、
、![]() 两点,是否存在定点
两点,是否存在定点![]() ,使得直线
,使得直线![]() 与
与![]() 斜率之积为定值,若存在,求出
斜率之积为定值,若存在,求出![]() 坐标;若不存在,请说明理由。
坐标;若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(Ⅰ)若![]() 的值域为
的值域为![]() ,求
,求![]() 的值;
的值;
(Ⅱ)巳![]() ,是否存在这祥的实数
,是否存在这祥的实数![]() ,使函数
,使函数![]() 在区间
在区间![]() 内有且只有一个零点.若存在,求出
内有且只有一个零点.若存在,求出![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a,b,c分别为△ABC三个内角A,B,C的对边,且acos C+![]() asin C-b-c=0.
asin C-b-c=0.
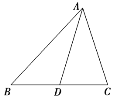
(1)求A;
(2)若AD为BC边上的中线,cos B=![]() ,AD=
,AD=![]() ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年辽宁省正式实施高考改革.新高考模式下,学生将根据自己的兴趣、爱好、学科特长和高校提供的“选考科目要求”进行选课.这样学生既能尊重自己爱好、特长做好生涯规划,又能发挥学科优势,进而在高考中获得更好的成绩和实现自己的理想.考改实施后,学生将在高二年级将面临着![]() 的选课模式,其中“3”是指语、数、外三科必学内容,“1”是指在物理和历史中选择一科学习,“2”是指在化学、生物、地理、政治四科中任选两科学习.某校为了更好的了解学生对“1”的选课情况,学校抽取了部分学生对选课意愿进行调查,依据调查结果制作出如下两个等高堆积条形图:根据这两幅图中的信息,下列哪个统计结论是不正确的( )
的选课模式,其中“3”是指语、数、外三科必学内容,“1”是指在物理和历史中选择一科学习,“2”是指在化学、生物、地理、政治四科中任选两科学习.某校为了更好的了解学生对“1”的选课情况,学校抽取了部分学生对选课意愿进行调查,依据调查结果制作出如下两个等高堆积条形图:根据这两幅图中的信息,下列哪个统计结论是不正确的( )
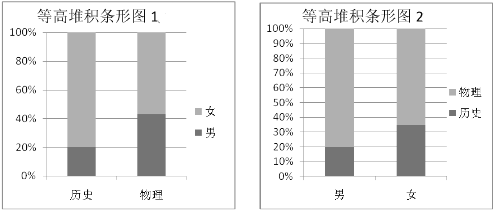
A.样本中的女生数量多于男生数量
B.样本中有学物理意愿的学生数量多于有学历史意愿的学生数量
C.样本中的男生偏爱物理
D.样本中的女生偏爱历史
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com