
【题目】若不等式![]() 在(0,+∞)上恒成立,则a的取值范围是________.
在(0,+∞)上恒成立,则a的取值范围是________.
【答案】[![]() ,+∞)
,+∞)
【解析】设![]() ,则
,则![]() ,(i)当a≤0时,
,(i)当a≤0时, ![]() ,则
,则![]() 在(0,+∞)上单调递增,所以
在(0,+∞)上单调递增,所以![]() 在(0,+∞)上恒成立,与已知不符,故a≤0不符合题意.
在(0,+∞)上恒成立,与已知不符,故a≤0不符合题意.
(jj )当 a>0 时,令![]() ,
, ![]() ,且
,且![]() ,①当2a≥1,即
,①当2a≥1,即![]() 时,
时, ![]() ,于是
,于是![]() 在 (0,+∞)上单调递减,所以
在 (0,+∞)上单调递减,所以![]() ,即
,即![]() 在
在![]() 上成立.则f(x)在
上成立.则f(x)在![]() 上单调递减,故f(x)< f (0)=0在(0,+∞)上成立,符合题意.②当0<2a<1,即0<a<
上单调递减,故f(x)< f (0)=0在(0,+∞)上成立,符合题意.②当0<2a<1,即0<a<![]() 时,
时, ![]() ,
, 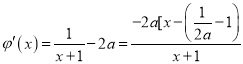 ,若
,若![]() ,则
,则![]() ,
, ![]() 在
在![]() 上单调递増;若在
上单调递増;若在![]() ,则
,则![]() ,
, ![]() 在
在![]() 上单调递减,又
上单调递减,又![]() ,则
,则![]() 在
在![]() 上成立,即
上成立,即![]() 在
在![]() 上恒成立,所以
上恒成立,所以![]() 在
在![]() 上单调递增,则
上单调递增,则![]() 在
在![]() 上恒成立.与已知不符,故0<a<
上恒成立.与已知不符,故0<a<![]() 不符合题意.综上所述,a的取值范围[
不符合题意.综上所述,a的取值范围[![]() ,+∞).
,+∞).
故答案为[![]() ,+∞).
,+∞).


科目:高中数学 来源: 题型:
【题目】一个盒子中装有6个完全相同的小球,分别标号为1,2,3,4,5,6.
(1)一次取出两个小球,求其号码之和能被3整除的概率;
(2)有放回的取球两次,每次取一个,求两个小球号码是相邻整数的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在空间中,下列命题正确的是
A.如果一个角的两边和另一角的两边分别平行,那么这两个角相等
B.两条异面直线所成的有的范围是![]()
C.如果两个平行平面同时与第三个平面相交,那么它们的交线平行
D.如果一条直线和平面内的一条直线平行,那么这条直线和这个平面平行
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种产品的质量以其“无故障使用时间![]() (单位:小时)”衡量,无故障使用时间越大表明产品质量越好,且无故障使用时间大于3小时的产品为优质品,从某企业生产的这种产品中抽取100件,并记录了每件产品的无故障使用时间,得到下面试验结果:
(单位:小时)”衡量,无故障使用时间越大表明产品质量越好,且无故障使用时间大于3小时的产品为优质品,从某企业生产的这种产品中抽取100件,并记录了每件产品的无故障使用时间,得到下面试验结果:
无故障使用时间 |
|
|
|
频数 | 20 | 40 | 40 |
以试验结果中无故障使用时间落入各组的频率作为一件产品的无故障使用时间落入相应组的概率.
(1)从该企业任取两件这种产品,求至少有一件是优质品的概率;
(2)若该企业生产的这种产品每件销售利润![]() (单位:元)与其无故障使用时间
(单位:元)与其无故障使用时间![]() 的关系式为
的关系式为
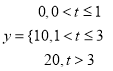
从该企业任取两件这种产品,其利润记为![]() (单位:元),求
(单位:元),求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
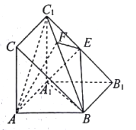
【题目】如图,直三棱柱ABC—A1B1C1中,侧面AA1B1B是正方形,AC丄侧面AA1B1B,AC=AB,点E是B1C1的中点.
(Ⅰ)求证:C1A∥平面EBA1;
(Ⅱ)若EF丄BC1,垂足为F,求二面角B—AF—A1的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4—4:坐标系与参数方程]
在平面直角坐标系xOy中,直线l的参数方程为 (t为参数),以平面直角坐标系的原点为极点,正半轴为极轴,取相同的长度单位建立极坐标系,曲线C的极坐标方程为
(t为参数),以平面直角坐标系的原点为极点,正半轴为极轴,取相同的长度单位建立极坐标系,曲线C的极坐标方程为![]() .
.
(Ⅰ)求直线l和曲线C的直角坐标方程,并指明曲线C的形状;
(Ⅱ)设直线l与曲线C交于A,B两点,O为坐标原点,且|OA|<|OB|,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在![]() 中,内角
中,内角![]() 、
、![]() 、
、![]() 所对的边分别是
所对的边分别是![]() 、
、![]() 、
、![]() ,不等式
,不等式![]() 对一切实数
对一切实数![]() 恒成立.
恒成立.
(1)求![]() 的取值范围;
的取值范围;
(2)当![]() 取最大值,且
取最大值,且![]() 的周长为
的周长为![]() 时,求
时,求![]() 面积的最大值,并指出面积取最大值时
面积的最大值,并指出面积取最大值时![]() 的形状.(参考知识:已知
的形状.(参考知识:已知![]() 、
、![]() ,
,![]() ;
;![]() 、
、![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中错误的个数是( )
①从某社区65户高收入家庭,280户中等收入家庭,105户低收入家庭中选出100户调查社会购买力的某一项指标,应采用的最佳抽样方法是分层抽样
②线性回归直线![]() 一定过样本中心点
一定过样本中心点![]()
③对于一组数据![]() ,如果将它们改变为
,如果将它们改变为![]() ,则平均数与方差均发生变化
,则平均数与方差均发生变化
④若一组数据1、![]() 、2、3的众数是2,则这组数据的中位数是2
、2、3的众数是2,则这组数据的中位数是2
⑤用系统抽样方法从编号为1,2,3,…,700的学生中抽样50人,若第2段中编号为20的学生被抽中,按照等间隔抽取的方法,则第5段中被抽中的学生编号为76
A.0B.1C.2D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com