
分析 ①利用对数的运算性质和运算法则求解.
②利用指数的运算性质和运算法则求解.
③把原式的角度600°变形为2×360°-120°,然后利用诱导公式化简,再把120°变为180°-60°,利用诱导公式及特殊角的三角函数值即可求出值.
④首先利用诱导公式将cos(-1020°)转化成cos60°,再利用特殊角函数值求出结果.
解答 解:①log2$\frac{1}{8}$=0-3=-3.
②$(\frac{16}{9})^{-\frac{3}{2}}$=($\frac{4}{3}$)${\;}^{2×(-\frac{3}{2})}$=$\frac{27}{64}$.
③sin600°=sin(2×360°-120°)=-sin120°=-sin(180°-60°)=-sin60°=-$\frac{\sqrt{3}}{2}$.
④cos(-1020°)=cos1020°=cos(3×2π°-60°)=cos60°=$\frac{1}{2}$.
点评 此题主要考查了对数及指数的运算性质和运算法则,运用诱导公式化简求值,熟练掌握诱导公式是解本题的关键,同时注意角度的灵活变换.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
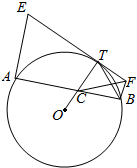 已知AB是圆O的一条弦,过点A、B分别作AE⊥AB,BF⊥AB,交弧AB上任意一点T的切线于点E、F,OT交AB于点C,求证:
已知AB是圆O的一条弦,过点A、B分别作AE⊥AB,BF⊥AB,交弧AB上任意一点T的切线于点E、F,OT交AB于点C,求证:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,+∞) | B. | (0,$\frac{3}{2}$) | C. | (0,$\frac{1}{2}$) | D. | ($\frac{1}{2}$,$\frac{3}{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com