
【题目】下列说法正确的是( )
A.![]() ,y
,y ![]() R,若x+y
R,若x+y ![]() 0,则x
0,则x ![]() 且y
且y ![]()
B.a ![]() R,“
R,“ ![]() ”是“a>1”的必要不充分条件
”是“a>1”的必要不充分条件
C.命题“ ![]() x
x ![]() R,使得
R,使得 ![]() ”的否定是“
”的否定是“ ![]() R,都有
R,都有 ![]() ”
”
D.“若 ![]() ,则a<b”的逆命题为真命题
,则a<b”的逆命题为真命题
【答案】B
【解析】A,x,y∈R,若x+y≠0,则x≠1且y≠﹣1的逆否命题为:x,y∈R,若x=1或y=﹣1,则x+y=0,为假命题,A不符合题意;
B,a∈R,“ ![]() ”“a<0,或a>1”是“a>1”的必要不充分条件,B符合题意;
”“a<0,或a>1”是“a>1”的必要不充分条件,B符合题意;
C,命题“x∈R,使得x2+2x+3<0”的否定是“x∈R,都有x2+2x+3≥0”,C不符合题意;
D,“若am2<bm2 , 则a<b”的逆命题为“若a<b,则am2<bm2”为假命题,D不符合题意;
故答案为:B
A,将原命题转化为逆否命题再进行判断,因为逆否命题与原命题同真假。
B,解出![]() 范围,然后比较两个范围的关系。
范围,然后比较两个范围的关系。
C,特称命题的否定是全称命题,只否定结论不否定条件,存在量词换为全称量词。
D,先将命题变为逆命题,再判断真假。


科目:高中数学 来源: 题型:
【题目】共享单车是指由企业在校园、公交站点、商业区、公共服务区等场所提供的自行车单车共享服务,由于其依托“互联网+”,符合“低碳出行”的理念,已越来越多地引起了人们的关注.某部门为了对该城市共享单车加强监管,随机选取了100人就该城市共享单车的推行情况进行问卷调查,并将问卷中的这100人根据其满意度评分值(百分制)按照[50,60),[60,70),…,[90,100]分成5组,制成如图所示频率分直方图. 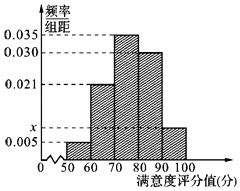
(Ⅰ) 求图中x的值;
(Ⅱ) 已知满意度评分值在[90,100]内的男生数与女生数的比为2:1,若在满意度评分值为[90,100]的人中随机抽取4人进行座谈,设其中的女生人数为随机变量X,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市电视台为了提高收视率而举办有奖问答活动,随机对该市15~65岁的人群抽样了 ![]() 人,回答问题统计结果及频率分布直方图如图表所示.
人,回答问题统计结果及频率分布直方图如图表所示.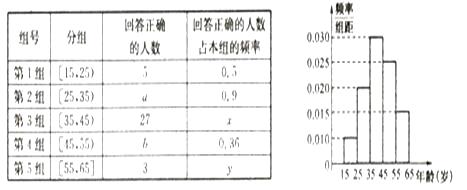
(1)分别求出 ![]() 的值;
的值;
(2)从第2,3,4组回答正确的人中用分层抽样的方法抽取6人,则第2,3,4组每组应各抽取多少人?
(3)在(2)的前提下,电视台决定在所抽取的6人中随机抽取2人颁发幸运奖,求所抽取的人中第2组至少有1人获得幸运奖的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的函数f(x)的图象关于y轴对称,且f(x)在[0,+∞)上单调递减,若关于x的不等式f(2mx﹣lnx﹣3)≥2f(3)﹣f(﹣2mx+lnx+3)在x∈[1,3]上恒成立,则实数m的取值范围为( )
A.[ ![]() ,
, ![]() ]
]
B.[ ![]() ,
, ![]() ]
]
C.[ ![]() ,
, ![]() ]
]
D.[ ![]() ,
, ![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数![]() 的图象的相邻两条对称轴之间的距离为
的图象的相邻两条对称轴之间的距离为![]() ,
,![]() ,则下列说法正确的是__________.(写出所有正确结论的序号)
,则下列说法正确的是__________.(写出所有正确结论的序号)
①![]() 是偶函数;
是偶函数;
②函数![]() 的图象关于点
的图象关于点![]() 对称;
对称;
③函数![]() 在
在![]() 上单调递增;
上单调递增;
④将函数![]() 的图象向右平移
的图象向右平移![]() 个单位长度,可得函数
个单位长度,可得函数![]() 的图象;
的图象;
⑤![]() 的对称轴方程为
的对称轴方程为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=cosx(![]() sinx+cosx)-
sinx+cosx)-![]() ,x∈R.
,x∈R.
(1)求函数f(x)的最小正周期和单调递增区间;
(2)设![]() >0,若函数g(x)=f(x+
>0,若函数g(x)=f(x+![]() )为奇函数,求
)为奇函数,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣ax+ ![]() ,其中a>0.
,其中a>0.
(Ⅰ)讨论函数f(x)的单调性;
(Ⅱ)证明:(1+ ![]() )(1+
)(1+ ![]() )(1+
)(1+ ![]() )…(1+
)…(1+ ![]() )<e
)<e ![]() (n∈N* , n≥2).
(n∈N* , n≥2).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com