Question

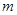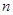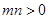对于常数、，“”是“方程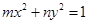的曲线是椭圆”的（    ）

A、充分不必要条件  B、必要不充分条件

C、充分必要条件    D、既不充分也不必要条件

 

Answer 1

【答案】

B

【解析】

试题分析：先根据mn＞0看能否得出方程mx²+ny²=1的曲线是椭圆；这里可以利用举出特值的方法来验证，再看方程mx²+ny²=1的曲线是椭圆，根据椭圆的方程的定义，可以得出mn＞0，即可得到结论．

当mn＞0时，方程mx²+ny²=1的曲线不一定是椭圆，

例如：当m=n=1时，方程mx²+ny²=1的曲线不是椭圆而是圆；或者是m，n都是负数，曲线表示的也不是椭圆；

故前者不是后者的充分条件；

当方程mx²+ny²=1的曲线是椭圆时，应有m，n都大于0，且两个量不相等，得到mn＞0；

由上可得：“mn＞0”是“方程mx²+ny²=1的曲线是椭圆”的必要不充分条件．

故选B．

考点：本试题主要考查了充分必要条件，考查椭圆的方程，注意对于椭圆的方程中，系数要满足大于0且不相等，本题是一个基础题。

点评：解决该试题的关键是理解椭圆的标准方程中,m,n的范围同正且不相等即可，以及将非标准的方程先化为标准的方程的形式。