
某兴趣小组测量电视塔AE的高度H(单位:m),如示意图,垂直放置的标杆BC的高度h=4m,仰角∠ABE= ,∠ADE=
,∠ADE= 。
。
(1) 该小组已经测得一组 、
、 的值,tan
的值,tan =1.24,tan
=1.24,tan =1.20,请据此算出H的值;
=1.20,请据此算出H的值;
(2) 该小组分析若干测得的数据后,认为适当调整标杆到电视塔的距离d(单位:m),使 与
与 之差较大,可以提高测量精确度。若电视塔的实际高度为125m,试问d为多少时,
之差较大,可以提高测量精确度。若电视塔的实际高度为125m,试问d为多少时,

 最大?
最大?
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:高中数学 来源: 题型:解答题
平面直角坐标系中有一个△ABC,角A,B,C所对应的边分别为 ,已知坐标原点与顶点B重合,且
,已知坐标原点与顶点B重合,且 ,
, ,
, =
= ,且∠A为锐角。(12分)
,且∠A为锐角。(12分)
(1)求角A的大小;
(2)若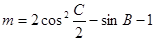 ,求实数
,求实数 的取值范围;
的取值范围;
(3)若 ,顶点A
,顶点A ,
,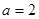 ,求△ABC的面积。
,求△ABC的面积。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分11分)在△ABC中,内角A,B,C对边的边长分别是a,b,c,已知c=2,C= .
.
(1)若△ABC的面积等于 ,求a,b;
,求a,b;
(2)若sinC+sin(B-A)=2sin2A,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分14分)
如图所示,在一个特定时段内,以点E为中心的10海里以内海域被设为警戒水域.点E正北40 海里处有一个雷达观测站A,某时刻测得一艘匀速直线行驶的船只位于点A北偏东30°且与点A相距100海里的位置B,经过2小时又测得该船已行驶到点A北偏东60°且与点A相距20
海里处有一个雷达观测站A,某时刻测得一艘匀速直线行驶的船只位于点A北偏东30°且与点A相距100海里的位置B,经过2小时又测得该船已行驶到点A北偏东60°且与点A相距20 海里的位置C.
海里的位置C.
(1)求该船的行驶速度(单位:海里/小时);
(2)若该船不改变航行方向继续行驶.判断它是否会进入警戒水域,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
12分)某城市有一块不规则的绿地如图所示,城建部门欲在该地上建造一个底座为三角形的环境标志,小李、小王设计的底座形状分别为△ABC、△ABD,经测量AD=BD=14,BC=10,AC=16,∠C=∠D.
(I)求AB的长度;
(Ⅱ)若建造环境标志的费用与用地面积成正比,不考虑其他因素,小李、小王谁的设计使建造费用最低,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com