
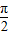 -B),此时有A=
-B),此时有A= -B,即A,B两角的和是直角,此时是直角三角形,若A是钝角,则有sin(π-A)=sin(
-B,即A,B两角的和是直角,此时是直角三角形,若A是钝角,则有sin(π-A)=sin( -B),可得A-B=
-B),可得A-B= ,如A=91°,B=1°时,亦有sinA=cosB,故三角形不一定是直角三角形.
,如A=91°,B=1°时,亦有sinA=cosB,故三角形不一定是直角三角形.

科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2011-2012年福建省福州市高二上学期期末考试理科数学 题型:填空题
.下列命题
①命题“事件A与B互斥”是“事件A与B对立”的必要不充分条件.
② “am2<bm2”是“a<b”的充分必要条件.
③ “矩形的两条对角线相等”的否命题为假.
④在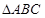 中,“
中,“ ”是
”是 三个角成等差数列的充要条件.
三个角成等差数列的充要条件.
⑤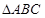 中,若
中,若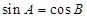 ,则
,则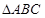 为直角三角形.
为直角三角形.
判断错误的有___________
查看答案和解析>>
科目:高中数学 来源:2010-2011年江西省高二下学期第二次月考数学理卷 题型:填空题
下列命题
①命题“事件A与B互斥”是“事件A与B对立”的必要不充分条件.
② “am2<bm2”是“a<b”的充分必要条件.
③ “矩形的两条对角线相等”的否命题为假.
④在 中,“
中,“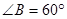 ”是
”是 三个角成等差数列的充要条件
三个角成等差数列的充要条件
⑤ 中,若
中,若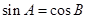 ,则
,则 为直角三角形.
为直角三角形.
判断错误的有___________
查看答案和解析>>
科目:高中数学 来源:2009-2010学年福建省四地六校高二(上)第二次联考数学试卷(理科)(解析版) 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com