【题目】某市甲、乙两地为了争创“市级文明城市”，现市文明委对甲、乙两地各派10名专家进行打分评优，所得分数情况如下茎叶图所示.
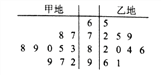
（1）分别计算甲、乙两地所得分数的平均值，并计算乙地得分的中位数；
（2）从乙地所得分数在
间的成绩中随机抽取2份做进一步分析，求所抽取的成绩中，至少有一份分数在
间的概率；
（3）在甲、乙两地所得分数超过90分的成绩中抽取其中2份分析其合理性，求这2份成绩都是来自甲地的概率.
【答案】（1）见解析；（2）
；（3）
.
【解析】分析：（1）由题得，结合所给的数据计算可得甲地得分的平均数为
，乙地得分的平均数为
，乙地得分的中位数为.
（2）由茎叶图可知，乙地得分中分数在
间的有四份成绩，随机抽取2份的情况有6种，其中至少有一份分数在
间的情况有5种.故所求概率.
（3）甲、乙两地所得分数中超过90分的一共有5份，随机抽取其中2份，共10种情况.其中两份成绩都来自甲地的有3种情况，故所求概率.
详解：（1）由题得，甲地得分的平均数为
，
乙地得分的平均数为
，
乙地得分的中位数为
.
（2）由茎叶图可知，乙地得分中分数在间的有65,72,75,79四份成绩，随机抽取2份的情况有：
，
，
，
，
，
，共6种，其中至少有一份分数在间的情况有：，，，，，共5种.故所求概率.
（3）甲、乙两地所得分数中超过90分的一共有5份，记甲地中的三份分别为
，乙地中的两份分别为
.随机抽取其中2份，所有情况如下：
，
，
，
，
，
，
，
，
，，一共10种.
其中两份成绩都来自甲地的有3种情况：，，，
故所求概率.
尖子生新课堂课时作业系列答案科目：高中数学 来源： 题型：
【题目】语文中有回文句，如：“上海自来水来自海上”，倒过来读完全一样。数学中也有类似现象，如：88，454，7337，43534等，无论从左往右读，还是从右往左读，都是同一个数，称这样的数为“回文数”！
二位的回文数有11，22，33，44，55，66，77，88，99，共9个；
三位的回文数有101，111，121，131，…，969，979，989，999，共90个；
四位的回文数有1001，1111，1221，…，9669，9779，9889，9999，共90个；
由此推测：11位的回文数总共有_________个．
查看答案和解析>>
科目：高中数学 来源： 题型：
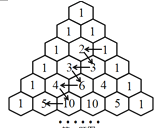
【题目】杨辉三角，是二项式系数在三角形中的一种几何排列。在欧洲，这个表叫做帕斯卡三角形。帕斯卡（1623----1662）是在1654年发现这一规律的，比杨辉要迟393年，比贾宪迟600年。右图的表在我国南宋数学家杨辉1261年所著的《详解九章算法》一书里就出现了，这又是我国数学史上的一个伟大成就。如图所示，在“杨辉三角”中，从1开始箭头所指的数组成一个锯齿形数列：1,2,3,3,6,4,10,5，…，则此数列前16项和为（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
．
（1）若
，
，求
的值域；
（2）当
时，求的最小值
；
（3）是否存在实数
、
，同时满足下列条件：① 
；② 当的定义域为
时，其值域为
．若存在，求出、的值；若不存在，请说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】自2016年底，共享单车日渐火爆起来，逐渐融入大家的日常生活中，某市针对18岁到80岁之间的不同年龄段的城市市民使用共享单车情况进行了抽样调查，结果如下表所示：
（1）采用分层抽样的方式从年龄在
内的人中抽取
人，求其中男性、女性的使用人数各为多少？
（2）在（1）中选出人中随机抽取4人，求其中恰有2人是女性的概率；
（3）用样本估计总体，在全市18岁到80岁的市民中抽4人其中男性使用的人数记为
，求的分布列。
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某电子产品生产企业生产一种产品，原计划每天可以生产
吨产品，每吨产品可以获得净利润
万元，其中
，由于受市场低迷的影响，该企业的净利润出现较大幅度下滑．为提升利润，该企业决定每天投入20万元作为奖金刺激生产．在此方案影响下预计每天可增产
吨产品，但是受原材料数量限制，增产量不会超过原计划每天产量的四分之一．试求在每天投入20万元奖金的情况下，该企业每天至少可获得多少利润(假定每天生产出来的产品都能销售出去)．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某兴趣小组有男生20人，女生10人，从中抽取一个容量为5的样本，恰好抽到2名男生和3名女生，则
①该抽样可能是系统抽样；
②该抽样可能是随机抽样：
③该抽样一定不是分层抽样；
④本次抽样中每个人被抽到的概率都是
．
其中说法正确的为（ ）
A.①②③B.②③C.②③④D.③④
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图（1），平面直角坐标系中，
的方程为
，
的方程为
，两圆内切于点
，动圆
与外切，与内切.
（1）求动圆圆心
的轨迹方程；
（2）如图（2），过点作的两条切线
，若圆心在直线
上的
也同时与相切，则称为的一个“反演圆”
（ⅰ）当
时，求证：的半径为定值；
（ⅱ）在（ⅰ）的条件下，已知
均与外切，与内切，且的圆心为
，求证：若的“反演圆”
相切，则也相切。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
