
【题目】已知函数f(x)=x3﹣12x.
(1)求f′(1)的值;
(2)求函数f(x)的单调区间.
【答案】
(1)解:因为f(x)=x3﹣12x,
所以f′(x)=3x2﹣12,所以f′(1)=﹣9
(2)解:f′(x)=3x2﹣12,
解f′(x)>0,得x<﹣2或x>2.
解f′(x)<0,得﹣2<x<2.
所以(﹣∞,﹣2)和(2,+∞)为函数f(x)的单调增区间,(﹣2,2)为函数f(x)的单调减区间
【解析】(1)求导数,即可求f′(1)的值;(2)求导数,利用导数的正负求函数f(x)的单调区间.
【考点精析】掌握基本求导法则和利用导数研究函数的单调性是解答本题的根本,需要知道若两个函数可导,则它们和、差、积、商必可导;若两个函数均不可导,则它们的和、差、积、商不一定不可导;一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减.
在这个区间单调递减.


科目:高中数学 来源: 题型:
【题目】规定投掷飞镖3次为一轮,若3次中至少两次投中8环以上为优秀,现采用随机模拟实验的方法估计某人投掷飞镖的情况:先由计算器产生随机数0或1,用0表示该次投标未在8环以上,用1表示该次投标在8环以上;再以每三个随机数作为一组,代表一轮的结果,经随机模拟实验产生了如下20组随机数:
101 111 011 101 010 100 100 011 111 110
000 011 010 001 111 011 100 000 101 101
据此估计,该选手投掷飞镖三轮,至少有一轮可以拿到优秀的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=loga(1+x),g(x)=loga(1﹣x)其中(a>0且a≠1),设h(x)=f(x)﹣g(x).
(1)求函数h(x)的定义域,判断h(x)的奇偶性,并说明理由;
(2)若f(3)=2,求使h(x)<0成立的x的集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的奇函数f(x),当x∈(﹣∞,0)时,f(x)=﹣x2+mx﹣1.
(1)求f(x)的解析式;
(2)若方程f(x)=0有五个不相等的实数解,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=x3﹣12x+4,x∈R.
(1)求f(x)的单调区间和极值;
(2)若关于x的方程f(x)=a有3个不同实根,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥P﹣ABCD中,AD∥BC,AD=AB=DC=![]()
![]() BC=1,E是PC的中点,面PAC⊥面ABCD.
BC=1,E是PC的中点,面PAC⊥面ABCD.

(1)证明:ED∥面PAB;
(2)若PC=2,PA=![]() ,求二面角A﹣PC﹣D的余弦值.
,求二面角A﹣PC﹣D的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在极坐标系![]() 中,已知曲线
中,已知曲线![]() :
: ![]() ,
, ![]() :
: ![]() ,
, ![]() :
: ![]() ,设
,设![]() 与
与![]() 交于点
交于点![]() .
.
(1)求点![]() 的极坐标;
的极坐标;
(2)若直线![]() 过点
过点![]() ,且与曲线
,且与曲线![]() 交于两不同的点
交于两不同的点![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() .
.
(1)若椭圆的离心率为![]() ,且点
,且点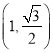 在椭圆上,①求椭圆的方程;
在椭圆上,①求椭圆的方程;
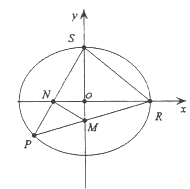
②设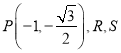 分别为椭圆
分别为椭圆![]() 的右顶点和上顶点,直线
的右顶点和上顶点,直线![]() 和
和![]() 与
与![]() 轴和
轴和![]() 轴相交于点
轴相交于点![]() ,求直线
,求直线![]() 的方程;
的方程;
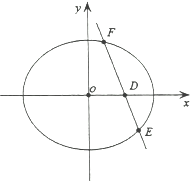
(2)设 ![]() 过
过![]() 点的直线
点的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,且
两点,且![]() 均在
均在![]() 的右侧,
的右侧, ![]() ,求椭圆离心率的取值范围.
,求椭圆离心率的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com