
【题目】在平面上,给定非零向量![]() ,对任意向量
,对任意向量![]() ,定义
,定义![]() .
.
(1)若![]() ,
,![]() ,求
,求![]() ;
;
(2)若![]() ,证明:若位置向量
,证明:若位置向量![]() 的终点在直线
的终点在直线![]() 上,则位置向量
上,则位置向量![]() 的终点也在一条直线上;
的终点也在一条直线上;
(3)已知存在单位向量![]() ,当位置向量
,当位置向量![]() 的终点在抛物线
的终点在抛物线![]() :
:![]() 上时,位置向量
上时,位置向量![]() 终点总在抛物线
终点总在抛物线![]() :
:![]() 上,曲线
上,曲线![]() 和
和![]() 关于直线
关于直线![]() 对称,问直线
对称,问直线![]() 与向量
与向量![]() 满足什么关系?
满足什么关系?
【答案】(1)![]() (2)见证明 (3)直线
(2)见证明 (3)直线![]() 与向量
与向量![]() 垂直
垂直
【解析】
(1)根据题意,算出![]() 7,
7,![]() 10,代入
10,代入![]() 的表达式并化简整理,即可得到
的表达式并化简整理,即可得到![]() (
(![]() ,
,![]() );(2)设
);(2)设![]() (x',y'),终点在直线Ax+By+C=0上,由题中
(x',y'),终点在直线Ax+By+C=0上,由题中![]() 的表达式解出
的表达式解出![]() (x,y)满足的关系式,从而得到点(
(x,y)满足的关系式,从而得到点(![]() ,
,![]() )在直线Ax+By+C=0上,化简整理得到直线(3A+4B)x+(4A﹣3B)y﹣5C=0,说明向量
)在直线Ax+By+C=0上,化简整理得到直线(3A+4B)x+(4A﹣3B)y﹣5C=0,说明向量![]() 的终点也在一条直线上;(3)设
的终点也在一条直线上;(3)设![]() ,则
,则![]() ,取
,取![]() ,解出
,解出![]() 关于
关于![]() 和t的坐标形式,结合
和t的坐标形式,结合![]() 的终点在抛物线x2=y上且
的终点在抛物线x2=y上且![]() 终点在抛物线y2=x上,建立关于
终点在抛物线y2=x上,建立关于![]() 和t的方程,化简整理得到
和t的方程,化简整理得到![]() ±(
±(![]() ,
,![]() ).再由曲线C和C′关于直线l:y=x对称,算出l的方向向量
).再由曲线C和C′关于直线l:y=x对称,算出l的方向向量![]() 满足
满足![]()
![]() 0,从而得到直线l与向量
0,从而得到直线l与向量![]() 垂直.
垂直.
(1)根据题意,![]() 7,
7,![]() 10,∴
10,∴![]() .
.
(2)设![]() ,
,![]() ,则
,则
![]()
![]() ,
,
∴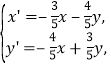
于是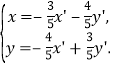 故
故![]() ,
,
从而![]() ,
,
由于![]() 、
、![]() 不全为零,所以
不全为零,所以![]() ,
,![]() 也不全为零.
也不全为零.
于是![]() 的终点在直线
的终点在直线![]() 上.
上.
(3)设![]() ,则
,则![]() ,对任意实数
,对任意实数![]() ,取
,取![]() ,
,
则![]()
![]()
![]() ,
,
∵![]() 的终点在曲线
的终点在曲线![]() 上,
上,
∴![]() .①
.①
由于![]() 为任意实数,比较①式两边
为任意实数,比较①式两边![]() 的系数得
的系数得
![]() ,
,![]() ,
,![]() ,
,
从而![]() ,
,![]() ,
,
∴![]() .
.
对曲线![]() 中任意点
中任意点![]() ,可知
,可知![]() 落在曲线
落在曲线![]() 上,反之亦然,故曲线
上,反之亦然,故曲线![]() :
:![]() 与曲线
与曲线![]() :
:![]() 关于直线
关于直线![]() :
:![]() 对称,
对称,
![]() 的方向向量
的方向向量![]() ,∵
,∵![]() ,∴
,∴![]() ,即直线
,即直线![]() 与向量
与向量![]() 垂直.
垂直.


科目:高中数学 来源: 题型:
【题目】计算机在数据处理时使用的是二进制,例如十进制数1,2,3,4的二进制数分别表示为1,10,11,100,二进制数…![]() 化为十进制数的公式为…
化为十进制数的公式为…![]()
![]() ,例如二进制数11等于十进制数
,例如二进制数11等于十进制数![]() ,又如二进制数101等于十进制数
,又如二进制数101等于十进制数![]() ,下图是某同学设计的将二进制数11111化为十进制数的程序框图,则判断框内应填入的条件是( )
,下图是某同学设计的将二进制数11111化为十进制数的程序框图,则判断框内应填入的条件是( )
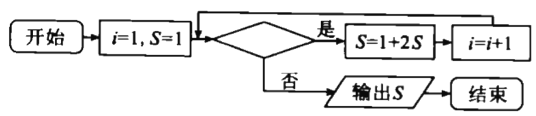
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,设
中,设![]() 为
为![]() :
:![]() 上的动点,点
上的动点,点![]() 为
为![]() 在
在![]() 轴上的投影,动点
轴上的投影,动点![]() 满足
满足![]() ,点
,点![]() 的轨迹为曲线
的轨迹为曲线![]() .以坐标原点为极点,
.以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() ,点
,点![]() ,
,![]() 为直线
为直线![]() 上两点.
上两点.
(1)求![]() 的参数方程;
的参数方程;
(2)是否存在![]() ,使得
,使得![]() 的面积为8?若存在,有几个这样的点?若不存在,请说明理由.
的面积为8?若存在,有几个这样的点?若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是周期为4的奇函数,且当
是周期为4的奇函数,且当![]() 时,
时,![]() ,方程
,方程![]() 在区间
在区间![]() 内有唯一解
内有唯一解![]() ,则方程
,则方程![]() 在区间
在区间![]() 上所有解的和为( )
上所有解的和为( )
A. ![]() B. 036162C. 3053234D. 3055252
B. 036162C. 3053234D. 3055252
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】由无理数论引发的数字危机一直延续到19世纪,直到1872年,德国数学家戴德金从连续性的要求出发,用有理数的“分割”来定义无理数(史称戴德金分割),并把实数理论建立在严格的科学基础上,才结束了无理数被认为“无理”的时代,也结束了持续2000多年的数学史上的第一次大危机,所谓戴德金分割,是指将有理数集![]() 划分为两个非空的子集
划分为两个非空的子集![]() 与
与![]() ,且满足
,且满足![]() ,
,![]() ,
,![]() 中的每一个元素都小于
中的每一个元素都小于![]() 中的每一个元素,则称
中的每一个元素,则称![]() 为戴德金分割.试判断,对于任一戴德金分割
为戴德金分割.试判断,对于任一戴德金分割![]() ,下列选项中,可能成立的是____.
,下列选项中,可能成立的是____.
①![]() 没有最大元素,
没有最大元素,![]() 有一个最小元素;②
有一个最小元素;②![]() 没有最大元素,
没有最大元素,![]() 也没有最小元素;
也没有最小元素;
③![]() 有一个最大元素,
有一个最大元素,![]() 有一个最小元素;④
有一个最小元素;④![]() 有一个最大元素,
有一个最大元素,![]() 没有最小元素.
没有最小元素.
查看答案和解析>>
科目:高中数学 来源: 题型:
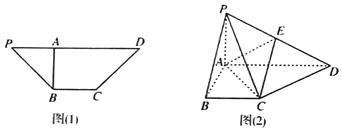
【题目】如图![]() 在四边形PBCD中,
在四边形PBCD中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,沿AB把三角形PAB折起,使P,D两点的距离为10,得到如图
,沿AB把三角形PAB折起,使P,D两点的距离为10,得到如图![]() 所示图形.
所示图形.
![]() Ⅰ
Ⅰ![]() 求证:平面
求证:平面![]() 平面PAC;
平面PAC;
![]() Ⅱ
Ⅱ![]() 若点E是PD的中点,求三棱锥
若点E是PD的中点,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校要通过选拔赛选取一名同学参加市级乒乓球单打比赛,选拔赛采取淘汰制,败者直接出局。现有两种赛制方案:三局两胜制和五局三胜制。问两选手对决时,选择何种赛制更有利于选拔出实力最强的选手,并说明理由。(设各局胜负相互独立,各选手水平互不相同。)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种“笼具”由内,外两层组成,无下底面,内层和外层分别是一个圆锥和圆柱,其中圆柱与圆锥的底面周长相等,圆柱有上底面,制作时需要将圆锥的顶端剪去,剪去部分和接头忽略不计,已知圆柱的底面周长为![]() ,高为
,高为![]() ,圆锥的母线长为
,圆锥的母线长为![]() .
.
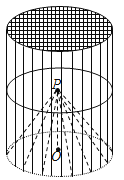
(1)求这种“笼具”的体积(结果精确到0.1![]() );
);
(2)现要使用一种纱网材料制作50个“笼具”,该材料的造价为每平方米8元,共需多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设有如下三个命题:
甲:相交直线l、m都在平面![]() 内,并且都不在平面
内,并且都不在平面![]() 内;
内;
乙:直线l、m中至少有一条与平面![]() 相交;
相交;
丙:平面![]() 与平面
与平面![]() 相交.
相交.
当甲成立时![]()
![]()
A. 乙是丙的充分而不必要条件
B. 乙是丙的必要而不充分条件
C. 乙是丙的充分且必要条件
D. 乙既不是丙的充分条件又不是丙的必要条件
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com