
【题目】对于数25,规定第1次操作为23+53=133,第2次操作为13+33+33=55,如此反复操作,则第2 017次操作后得到的数是( )
A. 25 B. 250
C. 55 D. 133
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:高中数学 来源: 题型:
【题目】扬州瘦西湖隧道长![]() 米,设汽车通过隧道的速度为
米,设汽车通过隧道的速度为![]() 米/秒
米/秒![]() .根据安全和车流的需要,当
.根据安全和车流的需要,当![]() 时,相邻两车之间的安全距离
时,相邻两车之间的安全距离![]() 为
为![]() 米;当
米;当![]() 时,相邻两车之间的安全距离
时,相邻两车之间的安全距离![]() 为
为![]() 米(其中
米(其中![]() 是常数).当
是常数).当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() .
.
(1)求![]() 的值;
的值;
(2)一列由![]() 辆汽车组成的车队匀速通过该隧道(第一辆汽车车身长为
辆汽车组成的车队匀速通过该隧道(第一辆汽车车身长为![]() 米,其余汽车车身长为
米,其余汽车车身长为![]() 米,每辆汽车速度均相同).记从第一辆汽车车头进入隧道,至第
米,每辆汽车速度均相同).记从第一辆汽车车头进入隧道,至第![]() 辆汽车车尾离开隧道所用的时间为
辆汽车车尾离开隧道所用的时间为![]() 秒.
秒.
①将![]() 表示为
表示为![]() 的函数;
的函数;
②要使车队通过隧道的时间![]() 不超过
不超过![]() 秒,求汽车速度
秒,求汽车速度![]() 的范围.
的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校某研究性学习小组在对学生上课注意力集中情况的调查研究中,发现其在40分钟的一节课中,注意力指数![]() 与听课时间
与听课时间![]() (单位:分钟)之间的关系满足如图所示的图象,当
(单位:分钟)之间的关系满足如图所示的图象,当![]() 时,图象是二次函数图象的一部分,其中顶点
时,图象是二次函数图象的一部分,其中顶点![]() ,过点
,过点![]() ;当
;当![]() 时,图象是线段
时,图象是线段![]() ,其中
,其中![]() .根据专家研究,当注意力指数大于62时,学习效果最佳.
.根据专家研究,当注意力指数大于62时,学习效果最佳.

(1)试求![]() 的函数关系式;
的函数关系式;
(2)教师在什么时段内安排内核心内容,能使得学生学习效果最佳?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
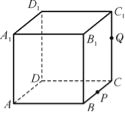
【题目】如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S,则下列命题正确的是 .(填序号)
①当0<CQ<![]() 时,S为四边形;
时,S为四边形;
②当CQ=![]() 时,S为等腰梯形;
时,S为等腰梯形;
③当CQ=![]() 时,S与C1D1的交点R满足C1R=
时,S与C1D1的交点R满足C1R=![]() ;
;
④当![]() <CQ<1时,S为六边形;
<CQ<1时,S为六边形;
⑤当CQ=1时,S的面积为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知方程![]() .
.
(1)若此方程表示圆,求![]() 的取值范围;
的取值范围;
(2)若(1)中的圆与直线![]() 相交于
相交于![]() ,
,![]() 两点,且
两点,且![]() (
(![]() 为坐标原点),求
为坐标原点),求![]() ;
;
(3)在(2)的条件下,求以![]() 为直径的圆的方程.
为直径的圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() 为其导函数,且
为其导函数,且![]() 时
时![]() 有极小值-9.
有极小值-9.
(1)求![]() 的单调递减区间;
的单调递减区间;
(2)若![]() ,
,![]() ,当
,当![]() 时,对于任意
时,对于任意![]() ,
,![]() 和
和![]() 的值至少有一个是正数,求实数
的值至少有一个是正数,求实数![]() 的取值范围;
的取值范围;
(3)若不等式![]() (
(![]() 为正整数)对任意正实数
为正整数)对任意正实数![]() 恒成立,求
恒成立,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 的三个顶点
的三个顶点![]() ,
,![]() ,
,![]() ,其外接圆为
,其外接圆为![]() .
.
(1)求![]() 的面积;
的面积;
(2)若直线![]() 过点
过点![]() ,且被
,且被![]() 截得的弦长为2,求直线
截得的弦长为2,求直线![]() 的方程;
的方程;
(3)对于线段![]() 上的任意一点
上的任意一点![]() ,若在以
,若在以![]() 为圆心的圆上都存在不同的两点
为圆心的圆上都存在不同的两点![]() ,
,![]() ,使得点
,使得点![]() 的线段
的线段![]() 的中点,求
的中点,求![]() 的半径
的半径![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ,
,![]() )的一系列对应值如表:
)的一系列对应值如表:

(1)根据表格提供的数据求函数![]() 的一个解析式;
的一个解析式;
(2)根据(1)的结果:
①当![]() 时,方程
时,方程![]() 恰有两个不同的解,求实数
恰有两个不同的解,求实数![]() 的取值范围;
的取值范围;
②若![]() ,
,![]() 是锐角三角形的两个内角,试比较
是锐角三角形的两个内角,试比较![]() 与
与![]() 的大小.
的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com