
分析 运用三角公式变形得出f(x)=)=$\sqrt{5-4cosφ}$sin(x+φ),根据三角函数的有界性得出:f(x)的最大值即可.
解答 解:函数f(x)=sin(x+2φ)-2sin(x+φ)
=(cosφ-2)sin(x+φ)+cos(x+φ)sin(φ)
=$\sqrt{(cosφ-2)^{2}+sin{φ}^{2}}$sin(x+φ+α)=$\sqrt{5-4cosφ}$sin(x+φ)
根据三角函数的有界性得出:f(x)的最大值为:$\sqrt{5-4cosφ}$
故答案为;$\sqrt{5-4cosφ}$.
点评 本题考查了三角函数公式的变形,正弦函数的有界性,关键是确定函数的基本形式,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(4.5)<f(6.5)<f(7) | B. | f(7)<f(6.5)<f(4.5) | C. | f(7)<f(4.5)<f(6.5) | D. | f(4.5)<f(7)<f(6.5) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a=a1•5-2 | B. | a=a1•2-3 | C. | a=a1•3-2 | D. | a=a1•2-5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (16,21) | B. | (16,24) | C. | (17,21) | D. | (18,24) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 250 | B. | -250 | C. | 150 | D. | -150 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
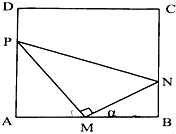 上海迪士尼乐园有一块长方形地ABCD,若要在此地块上拟建一个Rt△MNP的主题乐园,已知AB=2km,AD=$\sqrt{3}$km,点M是AB的中点,点P在线段AD上,点N在线段BC上,记∠NMB=α.
上海迪士尼乐园有一块长方形地ABCD,若要在此地块上拟建一个Rt△MNP的主题乐园,已知AB=2km,AD=$\sqrt{3}$km,点M是AB的中点,点P在线段AD上,点N在线段BC上,记∠NMB=α.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com