
| AC |
| BD |
| AB |
| a |
| AD |
| b |
| 1 |
| 2 |
| a |
| 1 |
| 2 |
| b |
科目:高中数学 来源:成功之路·突破重点线·数学(学生用书) 题型:013
在![]() ABCD中,AC=
ABCD中,AC=![]() ,BD=
,BD=![]() ,周长为18,则这个平行四边形的面积为
,周长为18,则这个平行四边形的面积为
[ ]
查看答案和解析>>
科目:高中数学 来源:《2.3 平面向量的基本定理及坐标表示》2013年同步练习1(解析版) 题型:选择题
 =
=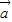 ,
,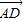 =
= ,
,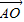 =λ1
=λ1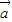 +λ2
+λ2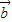 ,则λ1+λ2等于( )
,则λ1+λ2等于( )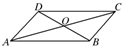


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com