
【题目】在平面直角坐标系![]() 中,已知抛物线
中,已知抛物线![]() 上的点
上的点![]() 到焦点
到焦点![]() 的距离为2.
的距离为2.
(1)求抛物线的方程;
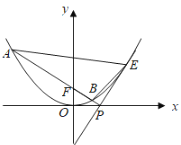
(2)如图,点![]() 是抛物线上异于原点的点,抛物线在点
是抛物线上异于原点的点,抛物线在点![]() 处的切线与
处的切线与![]() 轴相交于点
轴相交于点![]() ,直线
,直线![]() 与抛物线相交于
与抛物线相交于![]() 两点,求
两点,求![]() 面积的最小值.
面积的最小值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)求出抛物线![]() 的准线方程为
的准线方程为![]() ,由抛物线定义,得到
,由抛物线定义,得到![]() ,即可求解抛物线的方程.
,即可求解抛物线的方程.
(2)求出函数的![]() .设点
.设点![]() ,得到抛物线在点
,得到抛物线在点![]() 处的切线方程为
处的切线方程为![]() .求出
.求出![]() .推出直线
.推出直线![]() 的方程,点
的方程,点![]() 到直线
到直线![]() 的距离,联立
的距离,联立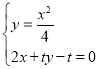 求出
求出![]() ,表示出
,表示出![]() 的面积,构造函数,通过函数的导数利用单调性求解最值即可.
的面积,构造函数,通过函数的导数利用单调性求解最值即可.
(1)抛物线![]() 的准线方程为
的准线方程为![]() ,
,
因为![]() ,由抛物线定义,知
,由抛物线定义,知![]() ,
,
所以![]() ,即
,即![]() ,
,
所以抛物线的方程为![]() .
.
(2)因为![]() ,所以
,所以![]() .
.
设点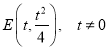 ,则抛物线在点
,则抛物线在点![]() 处的切线方程为
处的切线方程为![]() .
.
令![]() ,则
,则![]() ,即点
,即点![]() .
.
因为![]() 所以直线PF的方程为
所以直线PF的方程为![]() ,即
,即![]() .
.
则点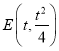 到直线
到直线![]() 的距离为
的距离为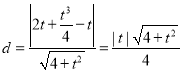 .
.
联立方程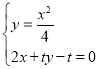 消元,得
消元,得![]() .
.
因为![]() ,
,
所以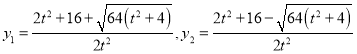 ,
,
所以![]() .
.
所以![]() 的面积为
的面积为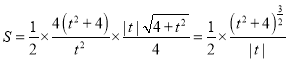 .
.
不妨设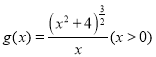 ,则
,则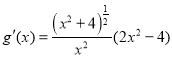 .
.
当![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 上单调递减;
上单调递减;
当![]() 上,
上,![]() ,所以
,所以![]() 在
在![]() 上单调递增,
上单调递增,
所以当![]() 时,
时,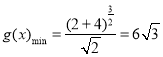 .
.
所以![]() 的面积的最小值为
的面积的最小值为![]() .
.


科目:高中数学 来源: 题型:
【题目】如下图,在四棱锥![]() 中,
中,![]() 面
面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点。
的中点。
(1)求证:![]() 面
面![]() ;
;
(2)线段![]() 上是否存在一点
上是否存在一点![]() ,满足
,满足![]() ?若存在,试求出二面角
?若存在,试求出二面角![]() 的余弦值;若不存在,说明理由。
的余弦值;若不存在,说明理由。

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某创新团队拟开发一种新产品,根据市场调查估计能获得10万元到1000万元的收益,先准备制定一个奖励方案:奖金![]() (单位:万元)随收益
(单位:万元)随收益![]() (单位:万元)的增加而增加,且奖金不超过9万元,同时奖金不超过收益的20%.
(单位:万元)的增加而增加,且奖金不超过9万元,同时奖金不超过收益的20%.
(1)若建立函数![]() 模型制定奖励方案,试用数学语言表示该团队对奖励函数
模型制定奖励方案,试用数学语言表示该团队对奖励函数![]() 模型的基本要求,并分析
模型的基本要求,并分析![]() 是否符合团队要求的奖励函数模型,并说明原因;
是否符合团队要求的奖励函数模型,并说明原因;
(2)若该团队采用模型函数![]() 作为奖励函数模型,试确定最小的正整数
作为奖励函数模型,试确定最小的正整数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 参数方程为
参数方程为![]() 为参数),将曲线
为参数),将曲线![]() 上所有点的横坐标变为原来的
上所有点的横坐标变为原来的![]() ,纵坐标变为原来的
,纵坐标变为原来的![]() ,得到曲线
,得到曲线![]() .
.
(1)求曲线![]() 的普通方程;
的普通方程;
(2)过点![]() 且倾斜角为
且倾斜角为![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 取得最小值时
取得最小值时![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率
的离心率![]() ,一个长轴顶点在直线
,一个长轴顶点在直线![]() 上,若直线
上,若直线![]() 与椭圆交于
与椭圆交于![]() ,
,![]() 两点,
两点,![]() 为坐标原点,直线
为坐标原点,直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() .
.
(1)求该椭圆的方程.
(2)若![]() ,试问
,试问![]() 的面积是否为定值?若是,求出这个定值;若不是,请说明理由.
的面积是否为定值?若是,求出这个定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】纸张的规格是指纸张制成后,经过修整切边,裁成一定的尺寸.现在我国采用国际标准,规定以![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 等标记来表示纸张的幅面规格.复印纸幅面规格只采用
等标记来表示纸张的幅面规格.复印纸幅面规格只采用![]() 系列和
系列和![]() 系列,其中系列的幅面规格为:①
系列,其中系列的幅面规格为:①![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 所有规格的纸张的幅宽(以
所有规格的纸张的幅宽(以![]() 表示)和长度(以
表示)和长度(以![]() 表示)的比例关系都为
表示)的比例关系都为![]() ;②将
;②将![]() 纸张沿长度方向对开成两等分,便成为
纸张沿长度方向对开成两等分,便成为![]() 规格,
规格,![]() 纸张沿长度方向对开成两等分,便成为
纸张沿长度方向对开成两等分,便成为![]() 规格,…,如此对开至
规格,…,如此对开至![]() 规格.现有
规格.现有![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 纸各一张.若
纸各一张.若![]() 纸的宽度为
纸的宽度为![]() ,则
,则![]() 纸的面积为________
纸的面积为________![]() ;这
;这![]() 张纸的面积之和等于________
张纸的面积之和等于________![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知函数![]() .(
.(![]() 是常数,且(
是常数,且(![]() )
)
(Ⅰ)求函数![]() 的单调区间;
的单调区间;
(Ⅱ)当![]() 在
在![]() 处取得极值时,若关于
处取得极值时,若关于![]() 的方程
的方程![]() 在
在![]() 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数![]() 的取值范围;
的取值范围;
(Ⅲ)求证:当![]() 时
时![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2021年我省将实施新高考,新高考“依据统一高考成绩、高中学业水平考试成绩,参考高中学生综合素质评价信息”进行人才选拔。我校2018级高一年级一个学习兴趣小组进行社会实践活动,决定对某商场销售的商品A进行市场销售量调研,通过对该商品一个阶段的调研得知,发现该商品每日的销售量![]() (单位:百件)与销售价格
(单位:百件)与销售价格![]() (元/件)近似满足关系式
(元/件)近似满足关系式![]() ,其中
,其中![]() 为常数
为常数![]() 已知销售价格为3元/件时,每日可售出该商品10百件。
已知销售价格为3元/件时,每日可售出该商品10百件。
(1)求函数![]() 的解析式;
的解析式;
(2)若该商品A的成本为2元/件,根据调研结果请你试确定该商品销售价格的值,使该商场每日销售该商品所获得的利润(单位:百元)最大。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com