
【题目】已知函数f(x)=asinxcosx﹣ ![]() acos2x+
acos2x+ ![]() a+b(a>0)
a+b(a>0)
(1)写出函数的单调递减区间;
(2)设x∈[0, ![]() ],f(x)的最小值是﹣2,最大值是
],f(x)的最小值是﹣2,最大值是 ![]() ,求实数a,b的值.
,求实数a,b的值.
【答案】
(1)解:f(x)=asinxcosx﹣ ![]() a
a ![]() =
= ![]() ﹣
﹣ ![]() +
+ ![]()
= ![]() ﹣
﹣ ![]() +b=asin(2x﹣
+b=asin(2x﹣ ![]() )+b.
)+b.
由 2kπ+ ![]() ≤2x﹣
≤2x﹣ ![]() ≤2kπ+
≤2kπ+ ![]() ,k∈z,解得 kπ+
,k∈z,解得 kπ+ ![]() ≤x≤kπ+
≤x≤kπ+ ![]() ,k∈z,
,k∈z,
故函数的单调递减区间为[kπ+ ![]() ,kπ+
,kπ+ ![]() ],k∈z
],k∈z
(2)解:∵x∈[0, ![]() ],∴﹣
],∴﹣ ![]() ≤2x﹣
≤2x﹣ ![]() ≤
≤ ![]() ,∴﹣
,∴﹣ ![]() ≤sin(2x﹣
≤sin(2x﹣ ![]() )≤1.
)≤1.
∴f(x)min = ![]() =﹣2,f(x)max =a+b=
=﹣2,f(x)max =a+b= ![]() ,
,
解得 a=2,b=﹣2+ ![]()
【解析】(1)利用三角函数的恒等变换化简f(x)的解析式等于asin(2x﹣ ![]() )+b,由 2kπ+
)+b,由 2kπ+ ![]() ≤2x﹣
≤2x﹣ ![]() ≤2kπ+
≤2kπ+ ![]() ,k∈z,求得x的范围即得函数的单调递减区间.(2)根据 x∈[0,
,k∈z,求得x的范围即得函数的单调递减区间.(2)根据 x∈[0, ![]() ],可得 2x﹣
],可得 2x﹣ ![]() 的范围,sin(2x﹣
的范围,sin(2x﹣ ![]() )的范围,根据f(x)的最小值是﹣2,最大值是
)的范围,根据f(x)的最小值是﹣2,最大值是 ![]() ,求得实数a,b的值.
,求得实数a,b的值.
【考点精析】认真审题,首先需要了解正弦函数的单调性(正弦函数的单调性:在![]()
![]() 上是增函数;在
上是增函数;在![]()
![]() 上是减函数),还要掌握三角函数的最值(函数
上是减函数),还要掌握三角函数的最值(函数![]() ,当
,当![]() 时,取得最小值为
时,取得最小值为![]() ;当
;当![]() 时,取得最大值为
时,取得最大值为![]() ,则
,则![]() ,
,![]() ,
,![]() )的相关知识才是答题的关键.
)的相关知识才是答题的关键.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(x2+x+m)ex(其中m∈R,e为自然对数的底数).若在x=﹣3处函数f (x)有极大值,则函数f (x)的极小值是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一次考试中,五位学生的数学,物理成绩如下表所示:

(1)要从5名学生中选2人参加一项活动,求选中的学生中至少有一人的物理成绩高于90分的概率;

(2)根据上表数据,画出散点图并用散点图说明物理成绩![]() 与数学成绩
与数学成绩![]() 之间线性相关关系的强弱,如果具有较强的线性相关关系,求
之间线性相关关系的强弱,如果具有较强的线性相关关系,求![]() 与
与![]() 的线性回归方程(系数精确到0.01);如果不具有线性相关关系,请说明理由.
的线性回归方程(系数精确到0.01);如果不具有线性相关关系,请说明理由.
参考公式:
回归直线的方程是![]() ,其中
,其中 ,
, ![]() ,
,
![]() 是与
是与![]() 对应的回归估计值,
对应的回归估计值,
参考数据: ![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知长为2的线段A B两端点A和B分别在x轴和y轴上滑动,线段AB的中点M的轨迹为曲线C. (Ⅰ)求曲线C的方程;
(Ⅱ)点P(x,y)是曲线C上的动点,求3x﹣4y的取值范围;
(Ⅲ)已知定点Q(0, ![]() ),探究是否存在定点T(0,t)(t
),探究是否存在定点T(0,t)(t ![]() )和常数λ满足:对曲线C上任意一点S,都有|ST|=λ|SQ|成立?若存在,求出t和λ;若不存在,请说明理由.
)和常数λ满足:对曲线C上任意一点S,都有|ST|=λ|SQ|成立?若存在,求出t和λ;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{ an}是一个公差大于0的等差数列,且满足a3a6=55,a2+a7=16.
(1)求数列{ an}的通项公式;
(2)若数列{bn}满足 ![]() +…+
+…+ ![]() =an (n∈N* ) 求数列{bn}的前n项和Sn .
=an (n∈N* ) 求数列{bn}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设等差数列{an}满足 ![]() =1,公差d∈(﹣1,0),当且仅当n=9时,数列{an}的前n项和Sn取得最大值,求该数列首项a1的取值范围( )
=1,公差d∈(﹣1,0),当且仅当n=9时,数列{an}的前n项和Sn取得最大值,求该数列首项a1的取值范围( )
A.( ![]() ,
, ![]() )
)
B.[ ![]() ,
, ![]() ]
]
C.( ![]() ,
, ![]() )
)
D.[ ![]() ,
, ![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某中学举行的物理知识竞赛中,将三个年级参赛学生的成绩在进行整理后分成5组,绘制出如图所示的频率分布直方图,图中从左到右依次为第一、第二、第三、第四、第五小组.已知第三小组的频数是15. 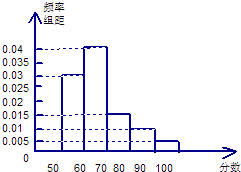
(1)求成绩在50~70分的频率是多少;
(2)求这三个年级参赛学生的总人数是多少;
(3)求成绩在80~100分的学生人数是多少.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知坐标平面上点M(x,y)与两个定点M1(26,1),M2(2,1)的距离之比等于5.
(1)求点M的轨迹方程,并说明轨迹是什么图形;
(2)记(1)中的轨迹为C,过点A(﹣2,3)的直线l被C所截得的线段的长为8,求直线l的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com