
分析 对任意不为零的实数a,b均有f(x0)=a+b成立等价于(2x-1)b=(1-2x2)a,分x=$\frac{1}{2}$或x≠$\frac{1}{2}$两种情况讨论,即可求出t的范围.
解答 解:f(x)=a+b成立等价于(2x-1)b=(1-2x2)a,
当x=$\frac{1}{2}$时,左边=0,右边≠0,不成立,
当x≠$\frac{1}{2}$时,(2x-1)b=(1-2x2)a等价于$\frac{b}{a}$=$\frac{1-2{x}^{2}}{2x-1}$,
设k=2x-1,则x=$\frac{k+1}{2}$,
则$\frac{b}{a}$=$\frac{1-\frac{(k+1)^{2}}{2}}{k}$=$\frac{-{k}^{2}-2k+1}{2k}$=$\frac{1}{2}$($\frac{1}{k}$-k-2),
∵x∈(0,t),(t<$\frac{1}{2}$),或x∈(0,$\frac{1}{2}$)∪($\frac{1}{2}$,t),(t>$\frac{1}{2}$),
∴k∈(-1,2t-1),(t<$\frac{1}{2}$),或k∈(-1,0)∪(0,2t-1),(t>$\frac{1}{2}$),(*)
∵?a,b∈R,
∴$\frac{b}{a}$=$\frac{1}{2}$($\frac{1}{k}$-k-2),在(*)上有解,
∴$\frac{1}{2}$($\frac{1}{k}$-k-2),在(*)上的值域为R,
设g(k)=$\frac{1}{2}$($\frac{1}{k}$-k)-1,则g(k)在(-∞,0),(0,+∞)上单调递减,
∴$\left\{\begin{array}{l}{t>\frac{1}{2}}\\{2t-1>1}\end{array}\right.$,
解得t>1,
故答案为:(1,+∞)
点评 本题考查了函数的单调性的应用,关键是构造函数,属于难题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (5,10) | B. | (-∞,5) | C. | (10,+∞) | D. | (-∞,5)∪(10,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
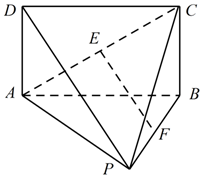 如图,在几何体P-ABCD中,平面ABCD⊥平面PAB,四边形ABCD为矩形,△PAB为正三角形,若AB=2,AD=1,E,F 分别为AC,BP中点.
如图,在几何体P-ABCD中,平面ABCD⊥平面PAB,四边形ABCD为矩形,△PAB为正三角形,若AB=2,AD=1,E,F 分别为AC,BP中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 31 | B. | 32 | C. | 63或$\frac{133}{27}$ | D. | 64 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com