
【题目】已知正方体![]() 的棱长为1,P是空间中任意一点,下列正确命题的个数是( )
的棱长为1,P是空间中任意一点,下列正确命题的个数是( )
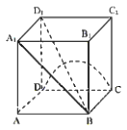
①若P为棱![]() 中点,则异面直线AP与CD所成角的正切值为
中点,则异面直线AP与CD所成角的正切值为![]() ;
;
②若P在线段![]() 上运动,则
上运动,则![]() 的最小值为
的最小值为![]() ;
;
③若P在半圆弧CD上运动,当三棱锥![]() 的体积最大时,三棱锥
的体积最大时,三棱锥![]() 外接球的表面积为
外接球的表面积为![]() ;
;
④若过点P的平面![]() 与正方体每条棱所成角相等,则
与正方体每条棱所成角相等,则![]() 截此正方体所得截面面积的最大值为
截此正方体所得截面面积的最大值为![]()
A.1个B.2个C.3个D.4个
【答案】C
【解析】
根据异面直线的夹角求解,棱锥外接球的求解,以及正方体截面的性质,对选项进行逐一分析即可.
对于①,如图所示,
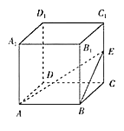
由![]() ,可知
,可知![]() 即为异面直线AE与CD所成的角.
即为异面直线AE与CD所成的角.
设正方体的棱长为2,连接BE,则在![]() 中,
中,![]() ,
,![]()
![]() ,故正确
,故正确
对于②,将三角形![]() 与四边形
与四边形![]() 沿
沿![]() 展开到同一个平面上,如图所示.
展开到同一个平面上,如图所示.

由图可知,线段![]() 的长度即为
的长度即为![]() 的最小值.
的最小值.
在![]() 中,利用余弦定理可得
中,利用余弦定理可得![]() ,故错误.
,故错误.
对于③,如下图所示:
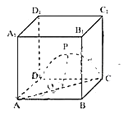
当P为![]() 中点时,三棱锥
中点时,三棱锥![]() 体积最大,
体积最大,
此时,三棱锥![]() 的外接球球心是AC中点,
的外接球球心是AC中点,
半径为![]() ﹐其表面积为
﹐其表面积为![]() .故正确.
.故正确.
对于④﹐平面![]() 与正方体的每条棱所在直线所成的角都相等,
与正方体的每条棱所在直线所成的角都相等,
只需与过同一顶点的三条棱所成的角相等即可,如图所示:
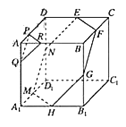
![]() .则平面PQR与正方体过点A的三条棱所成的角相等.
.则平面PQR与正方体过点A的三条棱所成的角相等.
若点E,F,G,H,M,N分别为相应棱的中点,
可得平面EFGHMN平行于平面PQR,且六边形EFGHMN为正六边形.
正方体棱长为1,所以正六边形EFGHMN的边长为![]() ,
,
可得此正六边形的面积为![]() ,为截面最大面积.
,为截面最大面积.
故正确的命题有3个.
故选:C.


科目:高中数学 来源: 题型:
【题目】某语文报社为研究学生课外阅读时间与语文考试中的作文分数的关系,随机调查了本市某中学高三文科班![]() 名学生每周课外阅读时间
名学生每周课外阅读时间![]() (单位:小时)与高三下学期期末考试中语文作文分数
(单位:小时)与高三下学期期末考试中语文作文分数![]() ,数据如下表:
,数据如下表:
| 1 | 2 | 3 | 4 | 5 | 6 |
| 38 | 40 | 43 | 45 | 50 | 54 |
(1)根据上述数据,求出高三学生语文作文分数![]() 与该学生每周课外阅读时间
与该学生每周课外阅读时间![]() 的线性回归方程,并预测某学生每周课外阅读时间为
的线性回归方程,并预测某学生每周课外阅读时间为![]() 小时时其语文作文成绩;
小时时其语文作文成绩;
(2)从这![]() 人中任选
人中任选![]() 人,这
人,这![]() 人中至少有
人中至少有![]() 人课外阅读时间不低于
人课外阅读时间不低于![]() 小时的概率.
小时的概率.
参考公式:![]() ,其中
,其中 ,
,![]()
参考数据:![]() ,
,![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】刍甍,中国古代算术中的一种几何图形,《九章算术》中记载“刍甍者,下有褒有广,而上有褒无广”刍,草也;甍,屋盖也.翻译为“底面有长有宽为矩形,顶部只有长没有宽为一条棱,刍甍字面意思为茅草屋顶”如图,为一刍甍的三视图,其中正视图为等腰梯形,侧视图为等腰三角形,若用茅草搭建它(无底面,不考虑厚度),则需要覆盖的面积至少为( )



A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019冠状病毒病(CoronaVirus Disease2019(COVID-19))是由新型冠状病毒(2019-nCoV)引发的疾病,目前全球感染者以百万计,我国在党中央、国务院、中央军委的坚强领导下,已经率先控制住疫情,但目前疫情防控形势依然严峻,湖北省中小学依然延期开学,所有学生按照停课不停学的要求,居家学习.小李同学在居家学习期间,从网上购买了一套高考数学冲刺模拟试卷,快递员计划在下午4:00~5:00之间送货到小区门口的快递柜中,小李同学父亲参加防疫志愿服务,按规定,他换班回家的时间在下午4:30~5:00,则小李父亲收到试卷无需等待的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥A﹣BCD中,点E在BD上,EA=EB=EC=ED,BD![]() CD,△ACD为正三角形,点M,N分别在AE,CD上运动(不含端点),且AM=CN,则当四面体C﹣EMN的体积取得最大值
CD,△ACD为正三角形,点M,N分别在AE,CD上运动(不含端点),且AM=CN,则当四面体C﹣EMN的体积取得最大值![]() 时,三棱锥A﹣BCD的外接球的表面积为_____.
时,三棱锥A﹣BCD的外接球的表面积为_____.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为椭圆
的焦点为椭圆![]() 的右焦点,C的准线与E交于P,Q两点,且
的右焦点,C的准线与E交于P,Q两点,且![]() .
.
(1)求E的方程;
(2)过E的左顶点A作直线l交E于另一点B,且BO(O为坐标原点)的延长线交E于点M,若直线AM的斜率为1,求l的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com