
【题目】函数![]() 是定义在
是定义在![]() 上的增函数,函数
上的增函数,函数![]() 的图象关于点
的图象关于点![]() 对称.若实数
对称.若实数![]() 满足不等式
满足不等式![]() ,则
,则![]() 的取值范围是_______.
的取值范围是_______.
科目:高中数学 来源: 题型:
【题目】判断下列对应是否为集合A到集合B的函数.
(1)A=R,B={x|x>0},f:x→y=|x|;
(2)A=Z,B=Z,f:x→y=x2;
(3)A=Z,B=Z,f:x→y=![]() ;
;
(4)A={x|-1≤x≤1},B={0},f:x→y=0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面直角坐标系中,已知曲线![]() ,将曲线
,将曲线![]() 上所有点横坐标,纵坐标分别伸长为原来的
上所有点横坐标,纵坐标分别伸长为原来的![]() 倍和
倍和![]() 倍后,得到曲线
倍后,得到曲线![]()
(1)试写出曲线![]() 的参数方程;
的参数方程;
(2)在曲线![]() 上求点
上求点![]() ,使得点
,使得点![]() 到直线
到直线![]() 的距离最大,并求距离最大值.
的距离最大,并求距离最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前三项与数列{bn}的前三项相同,且a1+2a2+22a3+…+2n-1an=8n对任意n∈N*都成立,数列{bn+1-bn}是等差数列.
(1)求数列{an}与{bn}的通项公式;
(2)是否存在k∈N*,使得(bk-ak)∈(0,1)?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 经过点
经过点![]() ,且离心率为
,且离心率为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设![]() 是椭圆上的点,直线
是椭圆上的点,直线![]() 与
与![]() (
(![]() 为坐标原点)的斜率之积为
为坐标原点)的斜率之积为![]() .若动点
.若动点![]() 满足
满足![]() ,试探究是否存在两个定点
,试探究是否存在两个定点![]() ,使得
,使得![]() 为定值?若存在,求
为定值?若存在,求![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】端午节吃粽子是我国的传统习俗.设一盘中装有10个粽子,其中豆沙粽2个,肉粽3个,白粽5个,这三种粽子的外观完全相同.从中任意选取3个.
(1)求三种粽子各取到1个的概率;
(2)设X表示取到的豆沙粽个数,求X的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】生活经验告诉我们,当水注进容器(设单位时间内进水量相同)时,水的高度随着时间的变化而变化,在下图中请选择与容器相匹配的图像,A对应________;B对应________;C对应________;D对应________.
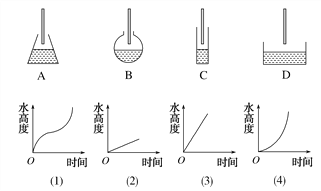
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com