
【题目】对于函数![]() 与
与![]() ,记集合
,记集合![]() ;
;
(1)设![]() ,
,![]() ,求
,求![]() .
.
(2)设![]() ,
,![]() ,若
,若![]() ,求实数a的取值范围.
,求实数a的取值范围.
(3)设![]() .如果
.如果![]() 求实数b的取值范围.
求实数b的取值范围.
【答案】(1)![]() 或
或![]() ; (2)
; (2)![]() ; (3)
; (3)![]() .
.
【解析】
(1)由题意,得到不等式![]() ,即可求解;
,即可求解;
(2)由![]() ,得出不等式
,得出不等式![]() 在
在![]() 上恒成立,利用二次函数的性质,分类讨论,即可求解;
上恒成立,利用二次函数的性质,分类讨论,即可求解;
③由![]() ,求得
,求得![]() ,又由
,又由![]() ,可得
,可得![]() ,分类讨论,使得
,分类讨论,使得![]() ,即可求解.
,即可求解.
(1)由题意,函数![]() ,
,![]() ,
,
令![]() ,即
,即![]() 或
或![]() ,解得
,解得![]() 或
或![]()
所以![]() 或
或![]() .
.
(2)由题意,函数![]() ,
,![]() ,
,
又由![]() ,即不等式
,即不等式![]() 的解集为
的解集为![]() ,
,
即![]() 在
在![]() 上恒成立,
上恒成立,
①当![]() 时,即
时,即![]() 时,不等式为
时,不等式为![]() 在
在![]() 上恒成立;
上恒成立;
②当![]() 时,则满足
时,则满足![]() 且
且![]() ,解得
,解得![]() ,
,
综上所述,实数![]() 的取值范围是
的取值范围是![]() .
.
③由题意,函数![]() ,
,
由![]() ,可得
,可得![]() ,解得
,解得![]() ,
,
又由![]() ,可得
,可得![]() ,
,
①当![]() 时,不等式
时,不等式![]() 的解集为
的解集为![]() ,要使得
,要使得![]() ,
,
则满足![]() ,即
,即![]() ,所以此时
,所以此时![]() ;
;
②当![]() 时,不等式
时,不等式![]() 的解集为
的解集为![]() 或
或![]() ,要使得
,要使得![]() ,
,
则满足![]() ,即
,即![]() ,所以此时
,所以此时![]() ;
;
③当![]() 时,不等式
时,不等式![]() 的解集为
的解集为![]() 或
或![]() ,要使得
,要使得![]() ,
,
则满足![]() 恒成立,所以此时
恒成立,所以此时![]() ,
,
综上所述,实数![]() 的取值范围是
的取值范围是![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】有一款手机,每部购买费用是5000元,每年网络费和电话费共需1000元;每部手机第一年不需维修,第二年维修费用为100元,以后每一年的维修费用均比上一年增加100元.设该款手机每部使用![]() 年共需维修费用
年共需维修费用![]() 元,总费用
元,总费用![]() 元.(总费用
元.(总费用![]() 购买费用
购买费用![]() 网络费和电话费
网络费和电话费![]() 维修费用)
维修费用)
(1)求函数![]() 、
、![]() 的表达式:
的表达式:
(2)这款手机每部使用多少年时,它的年平均费用最少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从甲、乙两名学生中选拔一人参加射箭比赛,为此需要对他们的射箭水平进行测试.现这两名学生在相同条件下各射箭10次,命中的环数如下:
甲 | 8 | 9 | 7 | 9 | 7 | 6 | 10 | 10 | 8 | 6 |
乙 | 10 | 9 | 8 | 6 | 8 | 7 | 9 | 7 | 8 | 8 |
(1)计算甲、乙两人射箭命中环数的平均数和标准差;
(2)比较两个人的成绩,然后决定选择哪名学生参加射箭比赛.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4―4:坐标系与参数方程]
在直角坐标系xOy中,曲线C的参数方程为![]() (θ为参数),直线l的参数方程为
(θ为参数),直线l的参数方程为![]() .
.
(1)若a=1,求C与l的交点坐标;
(2)若C上的点到l的距离的最大值为![]() ,求a.
,求a.
查看答案和解析>>
科目:高中数学 来源: 题型:
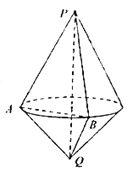
【题目】下图中的几何体是由两个有共同底面的圆锥组成.已知两个圆锥的顶点分别为P、Q,高分别为2、1,底面半径为1.A为底面圆周上的定点,B为底面圆周上的动点(不与A重合).下列四个结论:
①三棱锥![]() 体积的最大值为
体积的最大值为![]() ;
;
②直线PB与平面PAQ所成角的最大值为![]() ;
;
③当直线BQ与AP所成角最小时,其正弦值为![]() ;
;
④直线BQ与AP所成角的最大值为![]() ;
;
其中正确的结论有___________.(写出所有正确结论的编号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(12分)已知函数f(x)=![]()
(1)判断函数在区间[1,+∞)上的单调性,并用定义证明你的结论.
(2)求该函数在区间[1,4]上的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】样本(x1 , x2…,xn)的平均数为x,样本(y1 , y2 , …,ym)的平均数为 ![]() (
( ![]() ≠
≠ ![]() ).若样本(x1 , x2…,xn , y1 , y2 , …,ym)的平均数
).若样本(x1 , x2…,xn , y1 , y2 , …,ym)的平均数 ![]() =α
=α ![]() +(1﹣α)
+(1﹣α) ![]() ,其中0<α<
,其中0<α< ![]() ,则n,m的大小关系为( )
,则n,m的大小关系为( )
A.n<m
B.n>m
C.n=m
D.不能确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com