
【题目】已知函数![]() .
.
(1)试讨论![]() 的单调性;
的单调性;
(2)若函数在定义域上有两个极值点![]() ,试问:是否存在实数
,试问:是否存在实数![]() ,使得
,使得![]() ?
?
【答案】(1)见解析 (2)存在;![]()
【解析】
(1)求得函数的导数![]() ,结合基本不等式,分类讨论,即可得出函数的单调区间;
,结合基本不等式,分类讨论,即可得出函数的单调区间;
(2)由函数在定义域上有两个极值点![]() ,即方程
,即方程![]() 在
在![]() 上有两个不相等的实数根,转化为方程
上有两个不相等的实数根,转化为方程![]() 在
在![]() 上有两个不相等实数根
上有两个不相等实数根![]() ,结合二次函数的性质,求得
,结合二次函数的性质,求得![]() ,令
,令![]() ,即可求解.
,即可求解.
(1)由题意,函数![]() 的定义域为
的定义域为![]() ,
,
则![]()
![]() ,
,
因为![]() ,当且仅当
,当且仅当![]() ,即
,即![]() 时取“等号”,
时取“等号”,
所以![]() ,
,
当![]() 时,
时,![]() 在
在![]() 上恒成立,则此时
上恒成立,则此时![]() 在
在![]() 上单调递增,
上单调递增,
当![]() 时,
时,![]() ,
,
令![]() ,解得
,解得![]() ,
,![]() ,
,
由![]() ,
,
而![]() ,故
,故![]() .
.
由![]() 可得
可得![]() 或
或![]() ,
,
即此时![]() 在
在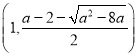 ,
,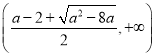 上单调递增;
上单调递增;
由![]() 可得
可得![]() ,
,
即此时![]() 在
在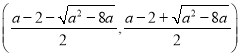 上单调递减;
上单调递减;
综上所述,当![]() 时,
时,![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,
时,![]() 在
在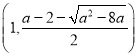 ,
,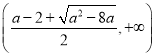 上单调递增,在
上单调递增,在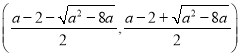 上单调递减.
上单调递减.
(2)因为![]() ,
,
由题知方程![]() 在
在![]() 上有两个不相等的实数根,
上有两个不相等的实数根,
即方程![]() 在
在![]() 上有两个不相等实数根
上有两个不相等实数根![]() ,
,
因此有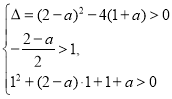 ,解得
,解得![]() ,
,
这时![]() ,
,![]() ,
,
于是![]()
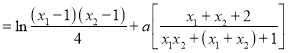
![]() .
.
令![]() ,解得
,解得![]() ,满足
,满足![]() .
.
所以存在实数![]() ,使得
,使得![]() .
.


科目:高中数学 来源: 题型:
【题目】马林●梅森是17世纪法国著名的数学家和修道士,也是当时欧洲科学界一位独特的中心人物,梅森在欧几里得、费马等人研究的基础上对2p﹣1作了大量的计算、验证工作,人们为了纪念梅森在数论方面的这一贡献,将形如2P﹣1(其中p是素数)的素数,称为梅森素数.若执行如图所示的程序框图,则输出的梅森素数的个数是( )
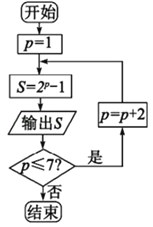
A.3B.4C.5D.6
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为直角梯形,
为直角梯形,![]() ,
,![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() ,
,![]() ,
,![]() .
.
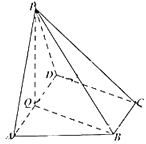
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若异面直线![]() 与
与![]() 所成角为
所成角为![]() ,求
,求![]() 的长;
的长;
(3)在(2)的条件下,求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合![]() ,若对于任意
,若对于任意![]() ,存在
,存在![]() ,使得
,使得![]() 成立,则称集合
成立,则称集合![]() 是“
是“![]() 集合”.给出下列5个集合:
集合”.给出下列5个集合:
①![]() ;②
;②![]() ;③
;③![]() ;
;
④![]() ;⑤
;⑤![]() .
.
其中是“![]() 集合”的所有序号是( )
集合”的所有序号是( )
A.②③B.①④⑤C.②③⑤D.①②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ln (x+1)-![]() -x,a∈R.
-x,a∈R.
(1)当a>0时,求函数f(x)的单调区间;
(2)若存在x>0,使f(x)+x+1<-![]() (a∈Z)成立,求a的最小值.
(a∈Z)成立,求a的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,点![]() 为圆
为圆![]() :
:![]() 上一动点,过点
上一动点,过点![]() 分别作
分别作![]() 轴,
轴,![]() 轴的垂线,垂足分别为
轴的垂线,垂足分别为![]() ,
,![]() ,连接
,连接![]() 延长至点
延长至点![]() ,使得
,使得![]() ,点
,点![]() 的轨迹记为曲线
的轨迹记为曲线![]() .
.
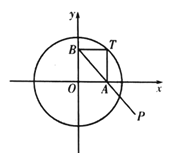
(1)求曲线![]() 的方程;
的方程;
(2)若点![]() ,
,![]() 分别位于
分别位于![]() 轴与
轴与![]() 轴的正半轴上,直线
轴的正半轴上,直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点,且
两点,且![]() ,试问在曲线
,试问在曲线![]() 上是否存在点
上是否存在点![]() ,使得四边形
,使得四边形![]() 为平行四边形,若存在,求出直线
为平行四边形,若存在,求出直线![]() 方程;若不存在,说明理由.
方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (
(![]() )经过点
)经过点![]() ,离心率为
,离心率为![]() ,
,![]() ,
,![]() 分别为椭圆的左、右焦点.
分别为椭圆的左、右焦点.
(1)求椭圆C的标准方程;
(2)若点![]() (
(![]() )在椭圆C上,求证;直线
)在椭圆C上,求证;直线![]() 与直线
与直线![]() 关于直线l:
关于直线l:![]() 对称.
对称.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com