
【题目】下列命题(1)![]() 条斜线段长相等,则他们在平面内的射影长也相等;(2)直线
条斜线段长相等,则他们在平面内的射影长也相等;(2)直线![]() 不在平面
不在平面![]() 内,他们在平面
内,他们在平面![]() 内的射影是两条平行直线,则
内的射影是两条平行直线,则![]() ;(3)与同一平面所成的角相等的两条直线平行;(4)一条直线与一个平面所成的角是
;(3)与同一平面所成的角相等的两条直线平行;(4)一条直线与一个平面所成的角是![]() ,那么它与平面内任何其他直线所成的角都不小于
,那么它与平面内任何其他直线所成的角都不小于![]() ;其中正确的命题序号是____________.
;其中正确的命题序号是____________.
【答案】(4)
【解析】
(1)(2)(3)根据数形结合,直观想象判断;(4)通过图象,构造线面角和线与其他线所成的角,通过这两个角的余弦值的大小判断角的关系.
(1)![]() 条斜线长相等,但与平面所成角不相等时,那么他们在平面内的射影长也不相等,故(1)错误;
条斜线长相等,但与平面所成角不相等时,那么他们在平面内的射影长也不相等,故(1)错误;
(2)如图,直线![]() 在平面
在平面![]() 内的两条射影平行,但
内的两条射影平行,但![]() 不一定平行,故(2)错误;
不一定平行,故(2)错误;
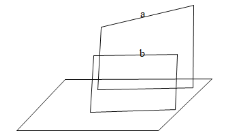
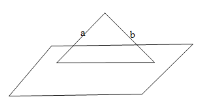
(3)与同一平面所成角相等的两条直线平行或相交,故(3)错误;
如图:直线![]() 与平面所成角相等,
与平面所成角相等,![]() 相交
相交
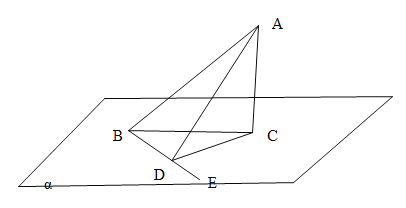
(4)如图,![]() 平面
平面![]() ,
,![]() 是平面
是平面![]() 的斜线,
的斜线,![]() 是平面内
是平面内![]() 以外的任一条直线,
以外的任一条直线,![]() ,
,![]() ,连接
,连接![]() ,
,
![]() ,
,![]() ,
,
又![]() ,
,![]()
![]() 平面
平面![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() 中,
中,![]()
![]() ,
,
![]() 和
和![]() 都在区间
都在区间![]() ,
,
![]() ,
,
当直线![]() 重合时,
重合时,![]() ,
,
当直线![]() 时,直线
时,直线![]() 与平面内的任意条直线所成的角都是
与平面内的任意条直线所成的角都是![]() ,
,
当线在平面内或与平面平行时,线与平面所成的角是![]() ,
,
综上:![]() ,故(4)正确.
,故(4)正确.
故答案为:(4)


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:
【题目】如图,在多面体ABD﹣A1B1C1D1中四边形A1B1C1D1,ADD1A1.ABB1A1均为正方形.点M是BD的中点.点H在线段C1M上,且A1H与平面ABD所成角的正弦值为![]() .
.
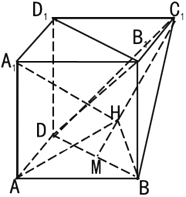
(Ⅰ)证明:B1D1∥平面BC1D:
(Ⅱ)求二面角A﹣A1H﹣B的的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() .数列
.数列![]() 满足
满足![]() ,
,![]() .
.
(1)若![]() ,且
,且![]() ,求正整数
,求正整数![]() 的值;
的值;
(2)若数列![]() ,
,![]() 均是等差数列,求
均是等差数列,求![]() 的取值范围;
的取值范围;
(3)若数列![]() 是等比数列,公比为
是等比数列,公比为![]() ,且
,且![]() ,是否存在正整数
,是否存在正整数![]() ,使
,使![]() ,
,![]() ,
,![]() 成等差数列,若存在,求出一个
成等差数列,若存在,求出一个![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)已知两个变量线性相关,若它们的相关性越强,则相关系数的绝对值越接近于1.
(2)线性回归直线必过点![]() ;
;
(3)对于分类变量A与B的随机变量![]() ,
,![]() 越大说明“A与B有关系”的可信度越大.
越大说明“A与B有关系”的可信度越大.
(4)在刻画回归模型的拟合效果时,残差平方和越小,相关指数![]() 的值越大,说明拟合的效果越好.
的值越大,说明拟合的效果越好.
(5)根据最小二乘法由一组样本点![]() ,求得的回归方程是
,求得的回归方程是![]() ,对所有的解释变量
,对所有的解释变量![]() ,
,![]() 的值一定与
的值一定与![]() 有误差.
有误差.
以上命题正确的序号为____________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过点![]() 作圆
作圆![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() ,直线
,直线![]() 恰好经过椭圆C:
恰好经过椭圆C:![]() 的右顶点和上顶点.
的右顶点和上顶点.
(1)求椭圆C方程;
(2)过椭圆C左焦点F的直线l交椭圆C于![]() 两点,椭圆上存在一点P,使得四边形
两点,椭圆上存在一点P,使得四边形![]() 为平行四边形,求直线l的方程。
为平行四边形,求直线l的方程。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在底面是菱形的四棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 在
在![]() 上,且
上,且![]() .
.
(1)证明:![]() 面
面![]() ;
;
(2)在棱![]() 上是否存在一点
上是否存在一点![]() ,使三棱锥
,使三棱锥![]() 是正三棱锥?证明你的结论.
是正三棱锥?证明你的结论.
(3)求以![]() 为棱,
为棱,![]() 与
与![]() 为面的二面角
为面的二面角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂对一批产品进行了抽样检测.右图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106],已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克并且小于104克的产品的个数是( ).
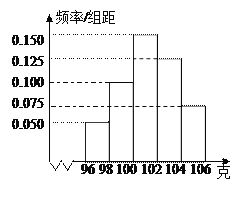
A. 90B. 75C. 60D. 45
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() ,直线
,直线![]() ,直线
,直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,点
,点![]() 和点
和点![]() 关于
关于![]() 轴对称,直线
轴对称,直线![]() 与
与![]() 轴交于点
轴交于点![]() .
.

(1)若点![]() 是椭圆
是椭圆![]() 的一个焦点,求该椭圆的长轴的长度;
的一个焦点,求该椭圆的长轴的长度;
(2)若![]() ,且
,且![]() ,求
,求![]() 的值;
的值;
(3)若![]() ,求证:
,求证:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l1:kx-y+4=0与直线l2:x+ky-3=0相交于点P,则当实数k变化时,点P到直线4x-3y+10=0的距离的最大值为( )
A.2B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com