
【题目】.魔术师从一个装有标号为1,2,3的小球的盒子中,无放回地变走两个小球,每次变走一个,先变走的小球的标号为m,后变走的小球的标号为n,这样构成有序数对(m,n).写出这个魔术的所有结果.
科目:高中数学 来源: 题型:
【题目】某城市理论预测2010年到2014年人口总数与年份的关系如下表所示
年份2010+x(年) | 0 | 1 | 2 | 3 | 4 |
人口数y(十万) | 5 | 7 | 8 | 11 | 19 |
(1)请根据上表提供的数据,求出y关于x的线性回归方程;
(2) 据此估计2015年该城市人口总数。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在甲、乙两个盒子中分别装有标号为1,2,3,4的四个球,现从甲乙两个盒子中各取出1个球,球的标号分别记做a,b,每个球被取出的可能性相等.
(1)求a+b能被3整除的概率;
(2)若|a-b|≤1则中奖,求中奖的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】拖延症总是表现在各种小事上,但日积月累,特别影响个人发展.某校的一个社会实践调查小组,在对该校学生进行“是否有明显拖延症”的调查中,随机发放了110份问卷.对收回的100份有效问卷进行统计,得到如下![]() 列联表:
列联表:
有明显拖延症 | 无明显拖延症 | 合计 | |
男 | 35 | 25 | 60 |
女 | 30 | 10 | 40 |
合计 | 65 | 35 | 100 |
(Ⅰ)按女生是否有明显拖延症进行分层,已经从40份女生问卷中抽取了8份问卷,现从这8份问卷中再随机抽取3份,并记其中无明显拖延症的问卷的份数为![]() ,试求随机变量
,试求随机变量![]() 的分布列和数学期望;
的分布列和数学期望;
(Ⅱ)若在犯错误的概率不超过![]() 的前提下认为无明显拖延症与性别有关,那么根据临界值表,最精确的
的前提下认为无明显拖延症与性别有关,那么根据临界值表,最精确的![]() 的值应为多少?请说明理由.
的值应为多少?请说明理由.
附:独立性检验统计量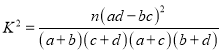 ,其中
,其中![]() .
.
独立性检验临界值表:
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 与双曲线
与双曲线![]() 有共同焦点,且离心率为
有共同焦点,且离心率为![]() .
.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)设![]() 为椭圆
为椭圆![]() 的下顶点,
的下顶点, ![]() 为椭圆上异于
为椭圆上异于![]() 的不同两点,且直线
的不同两点,且直线![]() 与
与![]() 的斜率之积为
的斜率之积为![]() .
.
(ⅰ)试问![]() 所在直线是否过定点?若是,求出该定点;若不是,请说明理由;
所在直线是否过定点?若是,求出该定点;若不是,请说明理由;
(ⅱ)若![]() 为椭圆
为椭圆![]() 上异于
上异于![]() 的一点,且
的一点,且![]() ,求
,求![]() 的面积的最小值.
的面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某项科研活动共进行了5次试验,其数据如下表所示:
特征量 | 第1次 | 第2次 | 第3次 | 第4次 | 第5次 |
| 555 | 559 | 551 | 563 | 552 |
| 601 | 605 | 597 | 599 | 598 |
(1)从5次特征量![]() 的试验数据中随机地抽取两个数据,求至少有一个大于600的概率;
的试验数据中随机地抽取两个数据,求至少有一个大于600的概率;
(2)求特征量![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;并预测当特征量
;并预测当特征量![]() 为570时特征量
为570时特征量![]() 的值.
的值.
(附:回归直线的斜率和截距的最小二乘法估计公式分别为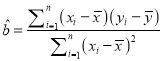 ,
, ![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com