
【题目】已知![]() 为坐标原点,对于函数
为坐标原点,对于函数![]() ,称向量
,称向量![]() 为函数
为函数![]() 的伴随向量,同时称函数
的伴随向量,同时称函数![]() 为向量
为向量![]() 的伴随函数.
的伴随函数.
(Ⅰ)设函数![]() ,试求
,试求![]() 的伴随向量
的伴随向量![]() ;
;
(Ⅱ)记向量![]() 的伴随函数为
的伴随函数为![]() ,求当
,求当![]() 且
且![]() 时
时![]() 的值;
的值;
(Ⅲ)由(Ⅰ)中函数![]() 的图像(纵坐标不变)横坐标伸长为原来的
的图像(纵坐标不变)横坐标伸长为原来的![]() 倍,再把整个图像向右平移
倍,再把整个图像向右平移![]() 个单位长度得到
个单位长度得到![]() 的图像。已知
的图像。已知![]()
![]() ,问在
,问在![]() 的图像上是否存在一点
的图像上是否存在一点![]() ,使得
,使得![]() .若存在,求出
.若存在,求出![]() 点坐标;若不存在,说明理由。
点坐标;若不存在,说明理由。
 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案科目:高中数学 来源: 题型:
【题目】某中学举行了一次“环保知识竞赛”, 全校学生参加了这次竞赛.为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)作为样本进行统计.请根据下面尚未完成并有局部污损的频率分布表和频率分布直方图(如图所示)解决下列问题:
![]()
| 分组 | 频数 | 频率 |
第1组 | [50,60) | 8 | 0 16 |
第2组 | [60,70) | a | ▓ |
第3组 | [70,80) | 20 | 0 40 |
第4组 | [80,90) | ▓ | 0 08 |
第5组 | [90,100] | 2 | b |
合计 | ▓ | ▓ |

(1)求出![]() 的值;
的值;
(2)在选取的样本中,从竞赛成绩是80分以上(含80分)的同学中随机抽取2名同学到广场参加环保知识的志愿宣传活动
(ⅰ)求所抽取的2名同学中至少有1名同学来自第5组的概率;
(ⅱ)求所抽取的2名同学来自同一组的概率
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市组织500名志愿者参加敬老活动,为方便安排任务将所有志愿者按年龄(单位:岁)分组,得到的频率分布表如下.现要从年龄较小的第1,2,3组中用分层抽样的方法抽取6人担任联系人.
年龄(岁) | 频率 | |
第1组 | [25,30) | 0.1 |
第2组 | [30,35) | 0.1 |
第3组 | [35,40) | 0.4 |
第4组 | [40,45) | 0.3 |
第5组 | [45,50) | 0.1 |
(I)应分别在第1,2,3组中抽取志愿者多少人?
(II)从这6人中随机抽取2人担任本次活动的宣传员,求至少有1人年龄在第3组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在以![]() 为顶点的五面体中,O为AB的中点,
为顶点的五面体中,O为AB的中点,
![]() 平面
平面![]() ,
, ![]() ∥
∥![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
(1)在图中过点O作平面![]() ,使得
,使得![]() ∥平面
∥平面![]() ,并说明理由;
,并说明理由;
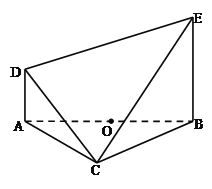
(2)求直线DE与平面CBE所成角的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
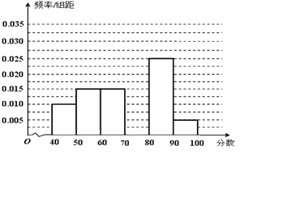
【题目】某校从参加考试的学生中抽出60名学生,将其成绩(均为整数)分成六组[40,50),[50,60), ...,[90,100]后画出如下部分频率分布直方图.观察图形的信息,回答下列问题:
(Ⅰ)求成绩落在[70,80)上的频率,并补全这个频率分布直方图;
(Ⅱ) 估计这次考试的及格率(60分及以上为及格)和平均分;
(Ⅲ) 从成绩在[40,50)和[90,100]的学生中任选两人,求他们在同一分数段的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x)是偶函数,对于x∈R都有f(x+6)=f(x)+f(3)成立.当x1,x2∈[0,3],且x1≠x2时,都有![]() >0,给出下列命题:
>0,给出下列命题:
① f(3)=0;
② 直线x=-6是函数y=f(x)的图象的一条对称轴;
③ 函数y=f(x)在[-9,-6]上为单调递减函数;
④ 函数y=f(x)在[-9,9]上有4个零点.
其中正确的命题是____________.(填序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知|a|=4,|b|=8,a与b的夹角是120°.
(1) 计算:① |a+b|,② |4a-2b|;
(2) 当k为何值时,(a+2b)⊥(ka-b)?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com