考点:棱柱、棱锥、棱台的体积,平面与平面垂直的判定
专题:空间位置关系与距离
分析:(1)以D为原点,DA为x轴,DC为y轴,DD
1为z轴,建立空间直角坐标系,利用向量法能证明平面EFH∥平面ABCD.
(2)求出平面BEF的法向量
=(a,b,c),从而求出C
1到平面BEF的距离,再由S
△BEF=
||•||sin<,>求出三角形BEF的面积,由此能求出三棱锥C
1-BEF的体积.
解答:
(1)证明:
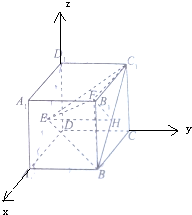
以D为原点,DA为x轴,DC为y轴,DD
1为z轴,
建立空间直角坐标系,
由已知得E(
,0,),F(0,
,),H(
,1,),
=(-
,
,0),
=(0,1,0),
设平面EFH的法向量为
=(x,y,z),
则
,∴
=(0,0,1),
又平面ABCD的法向量为
=(0,0,1),
∴平面EFH∥平面ABCD.
(2)解:B(1,1,0),C
1(0,1,1),
=(
,1,-),
=(-
,
,0),
=(-
,1,),
设平面BEF的法向量
=(a,b,c),
则
,
取a=1,得
=(1,1,3),
∴C
1到平面BEF的距离d=
=
=
,
|
|=
=
,|
|=
=
,
cos<
,>=
=
,
∴sin<
,>=
=
,
∴S
△BEF=
||•||sin<,>=
×××=
,
∴三棱锥C
1-BEF的体积V=
×S△BEF×d=
××=
.
点评:本题考查平面与平面平行的证明,考查三棱锥的体积的求法,是中档题,解题时要注意向量法的合理运用.

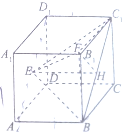 已知正方体ABCD-A1B1C1D1棱长为1,E、F、H分别为面A1ADD1、面DCC1D1与面BCC1B1的中心.
已知正方体ABCD-A1B1C1D1棱长为1,E、F、H分别为面A1ADD1、面DCC1D1与面BCC1B1的中心. 以D为原点,DA为x轴,DC为y轴,DD1为z轴,
以D为原点,DA为x轴,DC为y轴,DD1为z轴,

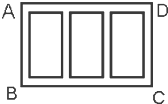 如图,某广场要划定一矩形区域ABCD,并在该区域内开辟出三块形状大小相同的小矩形绿化区,这三块绿化区四周和绿化区之间均设有1米宽的走道,已知三块绿化区的总面积为200平方米,求该矩形区域ABCD占地面积的最小值.
如图,某广场要划定一矩形区域ABCD,并在该区域内开辟出三块形状大小相同的小矩形绿化区,这三块绿化区四周和绿化区之间均设有1米宽的走道,已知三块绿化区的总面积为200平方米,求该矩形区域ABCD占地面积的最小值.