Question

【题目】在直三棱柱中， ,∠ACB=90°,Ｍ是 的中点，Ｎ是的中点．

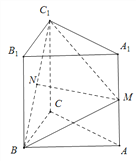
（Ⅰ）求证：MN∥平面；

（Ⅱ）求二面角的余弦值．

Answer 1

【答案】（Ⅰ）见解析；（Ⅱ） .

【解析】试题分析：（1）找中点构造平行四边形，然后根据线面平行的判定定理证明线面平行（2）要求二面角的余弦值应该先找出二面角的平面角，本题可以先找出要求角的补角，求出补角的余弦值，再求结果

解析：（Ⅰ）如图所示，取B1C1中点D，连结ND、A1D ∴DN∥BB1∥AA1

又DN＝ ∴四边形A1MND为平行四边形。

∴MN∥A1 D 又MN 平面A1B1C1,AD1平面A1B1C1 ∴MN∥平面-

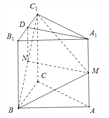
（Ⅱ）在平面ACC1A1上作CE⊥C1M交C1M于点E，A1C1于点F,

则CE为BE在平面ACC1A1上的射影，∴BE⊥C1M, ∴∠BEF为二面角B-C1M-A的平面角,

在等腰三角形CMC1中，CE=C1H=,∴tan∠BEC=

∴ cos∠BEC=.

二面角的平面角与∠BEC互补，所以二面角的余弦值为