
分析 :由题设知($\frac{m}{s}$+$\frac{n}{t}$)(s+t)=n+m+$\frac{mt}{s}$+$\frac{ns}{t}$≥m+n+2$\sqrt{\frac{mt}{s}•\frac{ns}{t}}$=m+n+2 $\sqrt{mn}$,满足 $\frac{mt}{s}$=$\frac{ns}{t}$时取最小值,由此得到m=n=1.设以(1,1)为中点的弦交椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{2}$=1于A(x1,y1),B(x2,y2),由中点从坐标公式知x1+x2=2,y1+y2=2,把A(x1,y1),B(x2,y2)分别代入x2+2y2=4,得2(x1-x2)+4(y1-y2)=0,k=$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$=-$\frac{1}{2}$,由此能求出此弦所在的直线方程.
解答 解:∵sm、n、s、t为正数,m+n=2,$\frac{m}{s}$+$\frac{n}{t}$=9,
s+t最小值是$\frac{4}{9}$,
∴($\frac{m}{s}$+$\frac{n}{t}$)(s+t)的最小值为4.
∴($\frac{m}{s}$+$\frac{n}{t}$)(s+t)=n+m+$\frac{mt}{s}$+$\frac{ns}{t}$≥m+n+2$\sqrt{\frac{mt}{s}•\frac{ns}{t}}$=m+n+2 $\sqrt{mn}$,
满足$\frac{mt}{s}=\frac{ns}{t}$时取最小值,
此时最小值为m+n+2$\sqrt{mn}$=2+2$\sqrt{mn}$=4,
得:mn=1,又:m+n=2,所以,m=n=1.
设以(1,1)为中点的弦交椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{2}$=1于A(x1,y1),B(x2,y2),
由中点从坐标公式知x1+x2=2,y1+y2=2,
把A(x1,y1),B(x2,y2)分别代入x2+2y2=4,得
$\left\{\begin{array}{l}{{{x}_{1}}^{2}+2{{y}_{1}}^{2}=4…①}\\{{{x}_{2}}^{2}+2{{y}_{2}}^{2}=4…②}\end{array}\right.$,
①-②,得2(x1-x2)+4(y1-y2)=0,
∴k=$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$=-$\frac{1}{2}$,
∴此弦所在的直线方程为y-1=-$\frac{1}{2}$(x-1),
即x+2y-3=0.
故答案为:x+2y-3=0.
点评 本题考查椭圆的性质和应用,解题时要认真审题,注意均值不等式和点差法的合理运用.


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:高中数学 来源: 题型:解答题
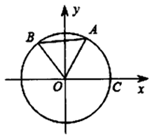 如图,在平面直角坐标系xoy中,A,B,C均为⊙O上的点,其中A($\frac{3}{5}$,$\frac{4}{5}$),C(1,0),点B在第二象限.
如图,在平面直角坐标系xoy中,A,B,C均为⊙O上的点,其中A($\frac{3}{5}$,$\frac{4}{5}$),C(1,0),点B在第二象限.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-1)∪(3,+∞) | B. | (1,3) | C. | (-1,3) | D. | (-∞,1)∪(3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,四边形OABC是边长为1的正方形,OD=3,点P为△BCD内(含边界)的动点,则|$\overrightarrow{OA}$+$\overrightarrow{OP}$|的取值范围为( )
如图,四边形OABC是边长为1的正方形,OD=3,点P为△BCD内(含边界)的动点,则|$\overrightarrow{OA}$+$\overrightarrow{OP}$|的取值范围为( )| A. | [$\frac{2\sqrt{10}}{5}$,5] | B. | [$\sqrt{2}$,4] | C. | [$\sqrt{2}$,$\sqrt{5}$] | D. | [$\frac{2\sqrt{10}}{5}$,4] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2018 | B. | 2017 | C. | 2016 | D. | 1008 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com