
生产A,B两种元件,其质量按测试指标划分为:指标大于或等于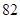 为正品,小于
为正品,小于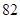 为次品.现随机抽取这两种元件各
为次品.现随机抽取这两种元件各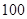 件进行检测,检测结果统计如下:
件进行检测,检测结果统计如下:
| 测试指标 |  | 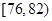 | 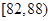 | 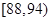 | 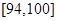 |
| 元件A | 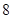 | 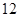 | 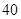 | 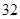 | 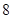 |
| 元件B | 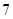 | 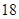 | 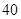 | 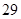 | 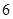 |
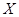 为生产1件元件A和1件元件B所得的总利润,求随机变量
为生产1件元件A和1件元件B所得的总利润,求随机变量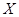 的分布列和数学期望;
的分布列和数学期望;科目:高中数学 来源: 题型:解答题
袋中有12个小球,分别为红球、黑球、黄球、绿球,从中任取一球,得到红球的概率为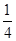 ,得到黑球或黄球的概率是
,得到黑球或黄球的概率是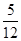 ,得到黄球或绿球的概率是
,得到黄球或绿球的概率是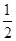 ,试求得到黑球、黄球、绿球的概率各是多少?
,试求得到黑球、黄球、绿球的概率各是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
甲、乙两人参加某种选拔测试.在备选的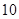 道题中,甲答对其中每道题的概率都是
道题中,甲答对其中每道题的概率都是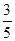 ,乙能答对其中的
,乙能答对其中的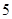 道题.规定每次考试都从备选的
道题.规定每次考试都从备选的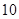 道题中随机抽出
道题中随机抽出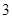 道题进行测试,答对一题加
道题进行测试,答对一题加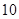 分,答错一题(不答视为答错)减
分,答错一题(不答视为答错)减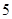 分,至少得
分,至少得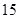 分才能入选.
分才能入选.
(1)求甲得分的数学期望;
(2)求甲、乙两人同时入选的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某校从高二年级学生中随机抽取60名学生,将其会考的政治成绩(均为整数)分成六段: 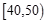 ,
,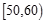 ,…,
,…,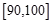 后得到如下频率分布直方图.
后得到如下频率分布直方图.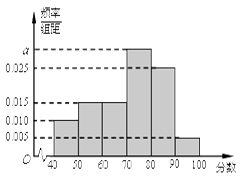
(Ⅰ)求图中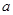 的值
的值
(Ⅱ)根据频率分布直方图,估计该校高二年级学生政治成绩的平均分;
(Ⅲ)用分层抽样的方法在80分以上(含 80分)的学生中抽取一个容量为6的样本,将该样本看成一个总体,从中任意选取2人,求其中恰有1人的分数不低于90分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
一个口袋中有质地、大小完全相同的5个球,编号分别为1,2,3,4,5,甲、乙两人玩一种游戏:甲先摸出一个球,记下编号,放回后乙再摸一个球,记下编号,如果两个编号的和为偶数算甲赢,否则算乙赢.
(Ⅰ)求甲赢且编号的和为6的事件发生的概率;
(Ⅱ)这种游戏规则公平吗?试用概率说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
市民李生居住在甲地,工作在乙地,他的小孩就读的小学在丙地,三地之间的道路情
况如图所示.假设工作日不走其它道路,只在图示的道路中往返,每次在路口选择道路是随机
的.同一条道路去程与回程是否堵车相互独立. 假设李生早上需要先开车送小孩去丙地小学,
再返回经甲地赶去乙地上班.假设道路 、
、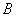 、
、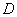 上下班时间往返出现拥堵的概率都是
上下班时间往返出现拥堵的概率都是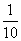 ,
,
道路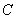 、
、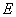 上下班时间往返出现拥堵的概率都是
上下班时间往返出现拥堵的概率都是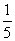 ,只要遇到拥堵上学和上班的都会迟到.
,只要遇到拥堵上学和上班的都会迟到.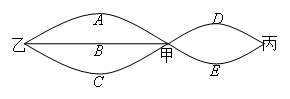
(1)求李生小孩按时到校的概率;
(2)李生是否有八成把握能够按时上班?
(3)设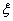 表示李生下班时从单位乙到达小学丙遇到拥堵的次数,求
表示李生下班时从单位乙到达小学丙遇到拥堵的次数,求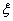 的均值.
的均值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设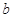 和
和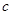 分别是先后抛掷一枚骰子得到的点数,用随机变量
分别是先后抛掷一枚骰子得到的点数,用随机变量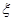 表示方程
表示方程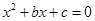 实根的个数(重根按一个计).
实根的个数(重根按一个计).
(1)求方程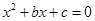 有实根的概率;
有实根的概率;
(2)求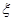 的分布列和数学期望;
的分布列和数学期望;
(3)求在先后两次出现的点数中有5的条件下,方程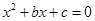 有实根的概率.
有实根的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
现有长分别为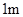 、
、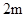 、
、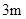 的钢管各
的钢管各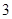 根(每根钢管质地均匀、粗细相同且附有不同的编号),从中随机抽取
根(每根钢管质地均匀、粗细相同且附有不同的编号),从中随机抽取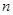 根(假设各钢管被抽取的可能性是均等的,
根(假设各钢管被抽取的可能性是均等的,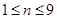 ),再将抽取的钢管相接焊成笔直的一根.
),再将抽取的钢管相接焊成笔直的一根.
(1)当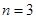 时,记事件
时,记事件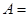 {抽取的
{抽取的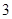 根钢管中恰有
根钢管中恰有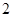 根长度相等},求
根长度相等},求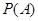 ;
;
(2)当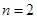 时,若用
时,若用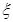 表示新焊成的钢管的长度(焊接误差不计),①求
表示新焊成的钢管的长度(焊接误差不计),①求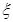 的分布列;
的分布列;
②令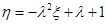 ,
,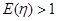 ,求实数
,求实数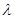 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com