
分析 (1)由已知得$\left\{\begin{array}{l}2c+2a=6\\ 2cb=ab\\{a^2}={b^2}+{c^2}\end{array}\right.$,解得a,b的值,可得椭圆C的方程;
(2)P(x0,y0),可得$\overrightarrow{{A}_{2}M}•\overrightarrow{{A}_{2}P}=0$,即以MP为直径的圆过点A2.
解答 (本小题满分14分)
解:(1)由已知得$\left\{\begin{array}{l}2c+2a=6\\ 2cb=ab\\{a^2}={b^2}+{c^2}\end{array}\right.$,解得$\left\{\begin{array}{l}a=2\\ b=\sqrt{3}\\ c=1\end{array}\right.$.
所以椭圆C的方程为$\frac{x^2}{4}+\frac{y^2}{3}=1$.…(5分)
证明:(Ⅱ)由题意知A1(-2,0),A2(2,0),…(6分)
设P(x0,y0),
则${l_{{A_1}P}}:y=\frac{y_0}{{{x_0}+2}}(x+2)$,得$M(14,\frac{{16{y_0}}}{{{x_0}+2}}))$.
且由点P在椭圆上,得${y_0}^2=3(1-\frac{{{x_0}^2}}{4})$.…(9分)
所以$\overrightarrow{{A_2}M}•\overrightarrow{{A_2}P}=(12,\frac{{16{y_0}}}{{{x_0}+2}})•({x_0}-2,{y_0})=12({x_0}-2)+\frac{{16{y_0}^2}}{{{x_0}+2}}$
=$12({x_0}-2)+\frac{{12(4-{x_0}^2)}}{{{x_0}+2}}=12({x_0}-2)-\frac{{12({x_0}-2)({x_0}+2)}}{{{x_0}+2}}=0$…(13分)
以MP为直径的圆过点A2.…(14分)
点评 本题考查的知识点是椭圆的标准方程,椭圆的简单性质,向量的数量积运算,难度中档.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{40\sqrt{10}}{3}$π | B. | $\frac{64\sqrt{2}}{3}$π | C. | $\frac{8\sqrt{2}}{3}$π | D. | 8π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{16}-\frac{y^2}{4}=1$ | B. | $\frac{x^2}{8}-\frac{y^2}{4}=1$ | C. | $\frac{x^2}{4}-{y^2}=1$ | D. | ${x^2}-\frac{y^2}{4}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
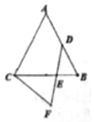 如图,△ABC为边长为1的正三角形,D为AB的中点,E在BC上,且BE:EC=1:2,连结DE并延长至F,使EF=DE,连结FC,则$\overrightarrow{FC}$•$\overrightarrow{AC}$的值为$\frac{7}{12}$.
如图,△ABC为边长为1的正三角形,D为AB的中点,E在BC上,且BE:EC=1:2,连结DE并延长至F,使EF=DE,连结FC,则$\overrightarrow{FC}$•$\overrightarrow{AC}$的值为$\frac{7}{12}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
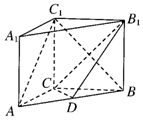 如图所示,在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点.
如图所示,在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$akm | B. | 2akm | C. | $\sqrt{5}$akm | D. | $\sqrt{7}$akm |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com