
【题目】已知四棱锥P﹣ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面 ABCD,且PA=AD=DB= ![]() ,AB=1,M是PB的中点.
,AB=1,M是PB的中点. 
(1)证明:面PAD⊥面PCD;
(2)求AC与PB所成的角;
(3)求平面AMC与平面BMC所成二面角的大小.
【答案】
(1)证明:∵PA⊥面ABCD,CD⊥AD,
∴由三垂线定理得:CD⊥PD.
因而,CD与面PAD内两条相交直线AD,PD都垂直,
∴CD⊥面PAD.
又CD面PCD,∴面PAD⊥面PCD
(2)解:过点B作BE∥CA,且BE=CA,则∠PBE是AC与PB所成的角.
连接AE,可知AC=CB=BE=AE= ![]() ,
,
又AB=2,所以四边形ACBE为正方形.
由PA⊥面ABCD,得∠PEB=90°
在Rt△PEB中,BE=a2=3b2,PB= ![]() ,
,
∴cos∠PBE= ![]() =
= ![]() .
.
∴AC与PB所成的角为arccos ![]()
(3)证明:作AN⊥CM,垂足为N,连接BN.
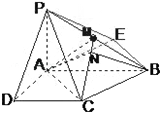
在Rt△PAB中,AM=MB,又AC=CB,
∴△AMC≌△BMC,
∴BN⊥CM,故∠ANB为所求二面角的平面角
∵CB⊥AC,
由三垂线定理,得CB⊥PC,
在Rt△PCB中,CM=MB,所以CM=AM.
在等腰三角形AMC中,ANMC= ![]() AC,
AC,
∴AN= 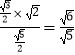 .∴AB=2,
.∴AB=2,
∴cos∠ANB= ![]() =﹣
=﹣ ![]() ,
,
故平面AMC与平面BMC所成二面角的大小为arccos(﹣ ![]() ).
).
【解析】(1)由三垂线定理得CD⊥PD,从而CD⊥面PAD,再由CD面PCD,能证明面PAD⊥面PCD. (2)过点B作BE∥CA,且BE=CA,则∠PBE是AC与PB所成的角. 连接AE,推导出四边形ACBE为正方形,由此能求出AC与PB所成的角.(3)作AN⊥CM,垂足为N,连接BN,则∠ANB为所求二面角的平面角,由此能求出平面AMC与平面BMC所成二面角的大小.
【考点精析】解答此题的关键在于理解异面直线及其所成的角的相关知识,掌握异面直线所成角的求法:1、平移法:在异面直线中的一条直线中选择一特殊点,作另一条的平行线;2、补形法:把空间图形补成熟悉的或完整的几何体,如正方体、平行六面体、长方体等,其目的在于容易发现两条异面直线间的关系,以及对平面与平面垂直的判定的理解,了解一个平面过另一个平面的垂线,则这两个平面垂直.


 习题精选系列答案
习题精选系列答案科目:高中数学 来源: 题型:
【题目】非空集合A中的元素个数用(A)表示,定义(A﹣B)= ![]() ,若A={﹣1,0},B={x||x2﹣2x﹣3|=a},且(A﹣B)≤1,则a的所有可能值为( )
,若A={﹣1,0},B={x||x2﹣2x﹣3|=a},且(A﹣B)≤1,则a的所有可能值为( )
A.{a|a≥4}
B.{a|a>4或a=0}
C.{a|0≤a≤4}
D.{a|a≥4或a=0}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列各组函数中不表示同一函数的是( )
A.f(x)=lgx2 , g(x)=2lg|x|
B.f(x)=x,g(x)= ![]()
C.f(x)= ![]() ,g(x)=
,g(x)= ![]()
![]()
D.f(x)=|x+1|,g(x)= ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,
, ![]() 在抛物线
在抛物线![]() 上,圆
上,圆![]() 过原点且与
过原点且与![]() 的准线相切.
的准线相切.
(Ⅰ) 求![]() 的方程;
的方程;
(Ⅱ) 点![]() ,点
,点![]() (与
(与![]() 不重合)在直线
不重合)在直线![]() 上运动,过点
上运动,过点![]() 作
作![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() ,
, ![]() .求证:
.求证: ![]() (其中
(其中![]() 为坐标原点).
为坐标原点).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() =1(a>b>0)的长轴是短轴的两倍,点P(
=1(a>b>0)的长轴是短轴的两倍,点P( ![]() ,
, ![]() )在椭圆上,不过原点的直线l与椭圆相交于A、B两点,设直线OA、l、OB的斜率分别为k1、k、k2 , 且k1、k、k2恰好构成等比数列,记△AOB的面积为S.
)在椭圆上,不过原点的直线l与椭圆相交于A、B两点,设直线OA、l、OB的斜率分别为k1、k、k2 , 且k1、k、k2恰好构成等比数列,记△AOB的面积为S. 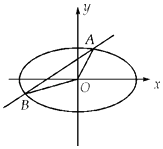
(1)求椭圆C的方程;
(2)试判断|OA|2+|OB|2是否为定值?若是,求出这个值;若不是,请说明理由?
(3)求△AOB面积S的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校![]() 届高三文(1)班在一次数学测验中,全班
届高三文(1)班在一次数学测验中,全班![]() 名学生的数学成绩的频率分布直方图如下,已知分数在
名学生的数学成绩的频率分布直方图如下,已知分数在![]() 的学生数有
的学生数有![]() 人.
人.
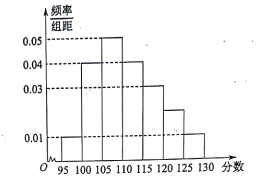
(1)求总人数![]() 和分数在
和分数在![]() 的人数
的人数![]() ;
;
(2)利用频率分布直方图,估算该班学生数学成绩的众数和中位数各是多少?
(3)现在从比分数在![]() 名学生(男女生比例为
名学生(男女生比例为![]() )中任选
)中任选![]() 人,求其中至多含有
人,求其中至多含有![]() 名男生的概率.
名男生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com