
【题目】已知f(x)是定义在R上的偶函数,f(x)在[0,+∞)上是增函数,且f( ![]() )=0,则不等式f(
)=0,则不等式f( ![]() )>0的解集为( )
)>0的解集为( )
A.(0, ![]() )∪(2,+∞)
)∪(2,+∞)
B.( ![]() ,1)∪(2,+∞)??
,1)∪(2,+∞)??
C.(0, ![]() )
)
D.(2,+∞)
【答案】A
【解析】解:方法1: 因为函数f(x)是定义在R上的偶函数,
所以不等式f( ![]() )>0等价为
)>0等价为 ![]() ,
,
因为函数f(x)在[0,+∞)上是增函数,且f( ![]() )=0,
)=0,
所以 ![]() ,即
,即 ![]() ,
,
即 ![]() 或
或 ![]() ,
,
解得 ![]() 或x>2.
或x>2.
方法2:已知f(x)是定义在R上的偶函数,f(x)在[0,+∞)上是增函数,且f( ![]() )=0,
)=0,
所以f(x)在(﹣∞,0]上是减函数,且f(﹣ ![]() )=0.①若
)=0.①若 ![]() ,则
,则 ![]() ,此时解得
,此时解得 ![]() .②若
.②若 ![]() ,则
,则 ![]() ,解得x>2.综上不等式f(
,解得x>2.综上不等式f( ![]() )>0的解集为(0,
)>0的解集为(0, ![]() )∪(2,+∞).
)∪(2,+∞).
故选A.
【考点精析】根据题目的已知条件,利用奇偶性与单调性的综合的相关知识可以得到问题的答案,需要掌握奇函数在关于原点对称的区间上有相同的单调性;偶函数在关于原点对称的区间上有相反的单调性.


 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】设f(x)是定义在R上的奇函数,且f(2)=0,当x>0时,有xf'(x)+f(x)<0恒成立,则不等式xf(x)>0的解集是( )
A.(﹣2,0)∪(2,+∞)
B.(﹣2,2)
C.(﹣∞,﹣2)∪(2,+∞)
D.(﹣2,0)∪(0,2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,E是PC的中点.求证: (Ⅰ)PA∥平面BDE;
(Ⅱ)平面PAC⊥平面BDE.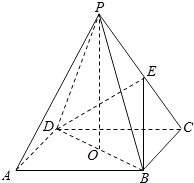
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】未来制造业对零件的精度要求越来越高. ![]() 打印通常是采用数字技术材料打印机来实现的,常在模具 制造、工业设计等领域被用于制造模型,后逐渐用于一些产品的直接制造,已经有使用这种技术打印而成的零部件.该技术应用十分广泛,可以预计在未来会有广阔的发展空间.某制造企业向
打印通常是采用数字技术材料打印机来实现的,常在模具 制造、工业设计等领域被用于制造模型,后逐渐用于一些产品的直接制造,已经有使用这种技术打印而成的零部件.该技术应用十分广泛,可以预计在未来会有广阔的发展空间.某制造企业向![]() 高校
高校![]() 打印实验团队租用一台
打印实验团队租用一台![]() 打印设备,用于打印一批对内径有较高精度要求的零件.该团队在实验室打印出了一批这样的零件,从中随机抽取10件零件,度量其内径的茎叶图如图所示(单位:
打印设备,用于打印一批对内径有较高精度要求的零件.该团队在实验室打印出了一批这样的零件,从中随机抽取10件零件,度量其内径的茎叶图如图所示(单位: ![]() ).
).
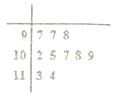
(1)计算平均值![]() 与标准差
与标准差![]() ;
;
(2)假设这台![]() 打印设备打印出品的零件内径
打印设备打印出品的零件内径![]() 服从正态分布
服从正态分布![]() ,在抽检零件中,如果出现了尺寸在
,在抽检零件中,如果出现了尺寸在![]() 之外的零件,就认为打印过程可能出现了异常情况,需对打印设备进行检查再调试.该团队到工厂安装调试后,试打了5个零件.度量其内径分别为(单位:
之外的零件,就认为打印过程可能出现了异常情况,需对打印设备进行检查再调试.该团队到工厂安装调试后,试打了5个零件.度量其内径分别为(单位: ![]() ): 86、95、103、109、118,试问此打印设备是否需要进一步调试,为什么?
): 86、95、103、109、118,试问此打印设备是否需要进一步调试,为什么?
参考数据: ![]() ,
, ![]() ,
,
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来空气质量逐步恶化,雾霾天气现象增多,大气污染危害加重,大气污染可引起心悸、呼吸困难等心肺疾病.为了解心肺疾病是否与性别有关,在市第一人民医院随机对入院50人进行了问卷调查,得到如下的列联表:
患心肺疾病 | 不患心肺疾病 | 合计 | |||||||||
男 | 20 | 5 | 25 | ||||||||
女 | 10 | 15 | 25 | ||||||||
合计 | 30 | 20 | 50 | ||||||||
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 | ||||
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 | ||||
(1)是否有99.5%的把握认为患心肺疾病与性别有关?说明你的理由;(2)已知在患心肺疾病的10位女性中,有3位又患有胃病,现在从患心肺疾病的10位女性中,选出3位进行其他方面的排查,其中患胃病的人数为![]() ,求
,求![]() 的分布列、数学期望.参考公式:
的分布列、数学期望.参考公式:![]() ,其中
,其中![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修44:坐标系与参数方程
在极坐标系中,点O(0,0), ![]() .
.
(1)求以![]() 为直径的圆
为直径的圆![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 的极坐标方程为
的极坐标方程为![]() ,判断直线
,判断直线![]() 与圆
与圆![]() 的位置关系.
的位置关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com