解:(I)函数f(x)的定义域是(0,+∞)
∵f(x)=x
2+(a-2)x-alnx,
∴f′(x)=2x+(a-2)-

=
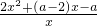
∵x=3是函数y=f(x)的极值点,
∴f′(3)=0,即
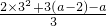
=0∴a=-6
检验:当a=-6时,f(x)=x
2-8x+6lnx,f′(x)=2x-8+

=
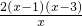
∴x∈(1,3)时,f′(x)<0,∈(3,+∞)时,f′(x)>0,此时,x=3是函数y=f(x)的极小值点.
∴当x=3是函数的极值点时,a=-6
(II)当a=-2时,f(x)=x
2-4x+2lnx(x>0),
∴f′(x)=2(x+

-2)≥0
∴曲线f(x)在定义域内的任意一点处的切线的斜率都大于等于0.
∴曲线f(x)可以与x-y+n=0中的一条直线相切
此时切线的斜率是1,
设切点坐标为(x
0,f(x
0)),则由f′(x
0)=1解得x
0=

或2.
∴切点坐标为(

,-2-2ln2),或(2,-4+ln2),
切线方程为x-y-2-2ln2=0或x-y-6+2ln2=0
(III)方程f(x)=(3a-2)x+alnx可化为x
2+(a-2)x-alnx=(3a-2)x+alnx
即x
2-2ax=2alnx
令函数g(x)=x
2-2ax,h(x)=2alnx
∴函数g(x)的图象与函数h(x)的图象当x>0时有唯一交点.
而当a>0时,g(x)图象开口向上,对称轴在y轴右侧,且过原点,
h(x)图象在y轴右侧,为过(1,0)点的增函数,两函数的图象一定有2个交点.
∴不在正实数a,使得关于x的方程f(x)=(3a-2)x+alnx有唯一实数解
分析:(I)若x=3是函数y=f(x)极值点,则x=3时导数一定为0,求出函数的导数,令导数等于0,解出a值即可.
(II)y=f(x)的切线斜率,时y=f(x)在切点出的导数,先求导,判断导数的正负,考虑哪条直线有可能是切线,
再根据导数值等于直线的斜率求切点坐标,若能求出,则存在,再求切线方程即可.
(III)把判断方程f(x)=(3a-2)x+alnx有唯一实数解的问题,转化为判断函数由唯一交点的问题,再借助二次函数与对数函数图象判断.
点评:本题考查了导数与极值之间的关系,导数几何意义的应用,以及利用函数图象判断方程的根的个数.

 =
=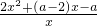
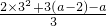 =0∴a=-6
=0∴a=-6 =
=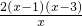
 -2)≥0
-2)≥0 或2.
或2. ,-2-2ln2),或(2,-4+ln2),
,-2-2ln2),或(2,-4+ln2),

 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<