
【题目】在四棱锥![]() 中,底面
中,底面![]() 为平行四边形,
为平行四边形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 点在底面
点在底面![]() 内的射影
内的射影![]() 在线段
在线段![]() 上,且
上,且![]() ,
, ![]() ,
, ![]() 为
为![]() 的中点,
的中点, ![]() 在线段
在线段![]() 上,且
上,且![]() .
.
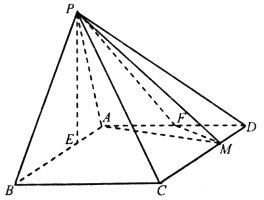
(Ⅰ)当![]() 时,证明:平面
时,证明:平面![]() 平面
平面![]() ;
;
(Ⅱ)当平面![]() 与平面
与平面![]() 所成的二面角的正弦值为
所成的二面角的正弦值为![]() 时,求四棱锥
时,求四棱锥![]() 的体积.
的体积.
【答案】(Ⅰ)见解析;(Ⅱ)![]() .
.
【解析】试题分析:(Ⅰ)接![]() ,作
,作![]() 交
交![]() 于点
于点![]() ,则四边形
,则四边形![]() 为平行四边形,在
为平行四边形,在![]() 中由余弦定理得
中由余弦定理得![]() ,由勾股定理可得
,由勾股定理可得![]() ,在
,在![]() 中,
中, ![]() ,
, ![]() 分别是
分别是![]() ,
, ![]() 的中点,结合中位线及平行的传递性可得
的中点,结合中位线及平行的传递性可得![]() ,故可得
,故可得![]() 平面
平面![]() ,由线面平行判定定理可得结论;(Ⅱ)以
,由线面平行判定定理可得结论;(Ⅱ)以![]() 为坐标原点,
为坐标原点, ![]() ,
, ![]() ,
, ![]() 所在直线分别为
所在直线分别为![]() 轴,
轴, ![]() 轴,
轴, ![]() 轴建立如图所示的空间直角坐标系,利用空间向量与二面角平面角之间关系可得:
轴建立如图所示的空间直角坐标系,利用空间向量与二面角平面角之间关系可得: ![]() ,由棱锥的体积公式可得结果.
,由棱锥的体积公式可得结果.
试题解析:(Ⅰ)证明:连接![]() ,作
,作![]() 交
交![]() 于点
于点![]() ,则四边形
,则四边形![]() 为平行四边形,
为平行四边形,
![]() ,在
,在![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,由余弦定理得
,由余弦定理得![]() .
.
所以![]() ,从而有
,从而有![]() .
.
在![]() 中,
中, ![]() ,
, ![]() 分别是
分别是![]() ,
, ![]() 的中点,
的中点,
则![]() ,
, ![]() ,
,
因为![]() ,所以
,所以![]() .
.
由![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
得![]() ,又
,又![]() ,
, ![]() ,
,
得![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]() .
.
(Ⅱ)以![]() 为坐标原点,
为坐标原点, ![]() ,
, ![]() ,
, ![]() 所在直线分别为
所在直线分别为![]() 轴,
轴, ![]() 轴,
轴, ![]() 轴建立如图所示的空间直角坐标系,则
轴建立如图所示的空间直角坐标系,则![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
平面![]() 的一个法向量为
的一个法向量为![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
由![]() ,
, ![]() ,得
,得![]() 令
令![]() ,得
,得![]() .
.
由题意可得, 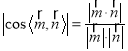
 ,
,
解得![]() ,
,
所以四棱锥![]() 的体积
的体积![]() .
.



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 若4Sn=(2n﹣1)an+1+1,且a1=1.
(1)求数列{an}的通项公式;
(2)设cn= ![]() ,数列{cn}的前n项和为Tn .
,数列{cn}的前n项和为Tn .
①求Tn;
②对于任意的n∈N*及x∈R,不等式kx2﹣6kx+k+7+3Tn>0恒成立,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)= ![]() sin2x+2cos2x+m在区间[0,
sin2x+2cos2x+m在区间[0, ![]() ]上的最大值为6,求常数m的值及此函数当x∈R时的最小值,并求相应的x的取值集合.
]上的最大值为6,求常数m的值及此函数当x∈R时的最小值,并求相应的x的取值集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位有工程师6人,技术员12人,技工18人,要从这些人中取一个容量为n的样本;如果采用系统抽样和分层抽样方法抽取,无须剔除个体;如果样本容量增加1个,则在采用系统抽样时需要在总体中先剔除一个个体,则n的值为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com