【题目】数列
满足
若
，则数列的前
项的和是__________．
【答案】450
【解析】分析：根据递推关系求出数列
的前几项，不难发现项的变化具有周期性，从而得到数列的前
项的和.
详解：∵数列{an}满足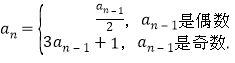
，
∵a1=34，∴a2=
=17，a3=3a2+1=3×17+1=52，a4=
=26，a5=
=13，a6=3a5+1=40，a7=
=20，a8=
=10，a9=
=5，a10=3a9+1=16，
a11=
=8，a12=
=4，a13=
=2，a14=
=1，同理可得：a15=4，a16=2，a17=1，……．
可得此数列从第12项开始为周期数列，周期为3．
则数列{an}的前100项的和=（a1+a2+……+a11）+a12+a13+29（a14+a15+a16）
=（34+17+52+26+13+40+20+10+5+16+8）+4+2+29×（1+4+2）
=450．
故答案为：450．
科目：高中数学 来源： 题型：
【题目】定义：由椭圆的两个焦点和短轴的一个顶点组成的三角形称为该椭圆的“特征三角形”；如果两个椭圆的“特征三角形”是相似的，则称这两个椭圆是“相似椭圆”，并将三角形的相似比称为椭圆的相似比，已知椭圆
.
（1）若椭圆
，判断
与
相似？如果相似，求出与的相似比；如果不相似，请说明理由；
（2）写出与椭圆相似且焦点在
轴上，短半轴长为
的椭圆
的标准方程；若在椭圆上存在两点
、
关于直线
对称，求实数的取值范围；
（3）如图：直线
与两个“相似椭圆”
和
分别交于点
和点
，试在椭圆和椭圆
上分别作出点
和点
（非椭圆顶点），使
和
组成以
为相似比的两个相似三角形，写出具体作法.（不必证明）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】经过坐标原点
的两条直线与椭圆
：
分别相交于点
、
和点
、
，其中直线
经过的左焦点
，直线
经过的右焦点
.当直线不垂直于坐标轴时，与
的斜率乘积为
.
（1）求椭圆的方程；
（2）求四边形
面积的最大值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】矩阵乘法运算
的几何意义为平面上的点
在矩阵
的作用下变换成点
，记
，且
.
（1）若平面上的点
在矩阵
的作用下变换成点
，求点的坐标；
（2）若平面上相异的两点、
在矩阵
的作用下，分别变换为点
、
，求证：若点
为线段
上的点，则点在的作用下的点
在线段
上；
（3）已知△
的顶点坐标为
、
、
，且△在矩阵
作用下变换成△
，记△与△的面积分别为
与
，求的值，并写出一般情况（三角形形状一般化且变换矩阵一般化）下与的关系（不要求证明）.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某中学2018年的高考考生人数是2015年高考考生人数的
倍，为了更好地对比该校考生的升学情况，统计了该校2015年和2018年的高考情况，得到如图柱状图：
则下列结论正确的是
A. 与2015年相比，2018年一本达线人数减少
B. 与2015年相比，2018年二本达线人数增加了
倍
C. 2015年与2018年艺体达线人数相同
D. 与2015年相比，2018年不上线的人数有所增加
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知抛物线
，圆
.
（Ⅰ）
是抛物线
的焦点，
是抛物线上的定点，
，求抛物线的方程；
（Ⅱ）在（Ⅰ）的条件下，过点的直线
与圆
相切，设直线交抛物线于
，
两点，则在
轴上是否存在点
使
？若存在，求出点的坐标；若不存在，请说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】近年来，智能手机的更新换代极其频繁和快速，而青少年对新事物的追求更是强烈，为了调查大学生更换手机的时间，现对某大学中的大学生使用一部手机的年限进行了问卷调查，并从参与调查的大学生中抽取了男生、女生各
人进行抽样分析，制成如下的频率分布直方图.
（1）根据频率分布直方图，估计男大学生使用手机年限的中位数和女大学生使用手机年限的众数；
（2）根据频率分布直方图，求出男大学生和女大学生使用手机年限的平均值，并分析比较男大学生和女大学生哪个群体更换手机的频率更高.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
