
分析 运用数学归纳法证明,注意解题步骤,特别是n=k+1时,运用假设n=k的结论,结合放缩法,即可得证
解答 证明:①当n=1时,左边=1,右边=$\frac{1}{2}$,不等式成立;
②假设n=k(k≥1且k∈N*)时不等式成立,即1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{{2}^{k}-1}$>$\frac{k}{2}$成立,
则当n=k+1时,因为1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{{2}^{k}-1}+\frac{1}{{2}^{k}}$+…+$\frac{1}{{2}^{k+1}-1}$>$\frac{k}{2}+\frac{1}{{2}^{k}}$+…+$\frac{1}{{2}^{k+1}-1}$
又因为$\frac{1}{{2}^{k}}$+…+$\frac{1}{{2}^{k+1}-1}$>$\frac{{2}^{k}}{{2}^{k+1}-1}$>$\frac{{2}^{k}}{{2}^{k+1}}$=$\frac{1}{2}$
所以1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{{2}^{k}-1}$+$\frac{1}{{2}^{k}}$+…+$\frac{1}{{2}^{k+1}-1}$>$\frac{k+1}{2}$
即当n=k+1时不等式成立
所以由①、②可知对所有 n∈N*原不等式成立;
点评 本题考查不等式的证明,主要考查数学归纳法证明不等式的方法,考查推理能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
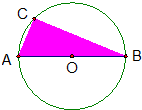 如图,点C为半径是1的圆上一点,且劣弧长AC是劣弧长CB的一半,假设你在这个图形上随机地撒一粒豆子,则∠ABC及豆子落在阴影区域的概率分别是( )
如图,点C为半径是1的圆上一点,且劣弧长AC是劣弧长CB的一半,假设你在这个图形上随机地撒一粒豆子,则∠ABC及豆子落在阴影区域的概率分别是( )| A. | $\frac{π}{6}$,$\frac{\sqrt{3}}{2π}$ | B. | $\frac{π}{3}$,$\frac{\sqrt{3}}{2π}$ | C. | $\frac{π}{6}$,$\frac{\sqrt{3}}{2}$ | D. | $\frac{π}{6}$,$\frac{3}{2π}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
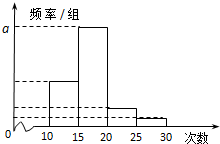 公司随机抽取M名员工作为样本,得到这M名员工参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
公司随机抽取M名员工作为样本,得到这M名员工参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:| 分组 | 频数 | 频率 |
| [10,15) | 10 | 0.25 |
| [15,20) | 24 | n |
| [20,25) | m | p |
| [25,30) | 2 | 0.05 |
| 合计 | M | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 22014-1 | B. | 22014+1 | C. | 22015-1 | D. | 22015+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①②③④ | B. | ①②④ | C. | ①③④ | D. | ②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com