
如图菱形ABEF所在平面与直角梯形ABCD所在平面互相垂直,AB=2AD=2CD=4,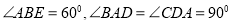 ,点H、G分别是线段EF、BC的中点.
,点H、G分别是线段EF、BC的中点.
(1)求证:平面AHC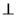 平面
平面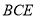 ;(2)(2)求此几何体的体积.
;(2)(2)求此几何体的体积.

(1)详见解析;(2)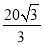 .
.
【解析】
试题分析:(1)要证面面垂直,首先证线面垂直.那么在本题中证哪条线垂直哪个面?结合条件可得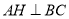 ,
,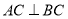 ,所以
,所以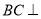 面AHC,从而平面AHC
面AHC,从而平面AHC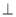 平面BCE.(2)可将该几何体切割为三部分:
平面BCE.(2)可将该几何体切割为三部分: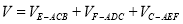 ,然后分别求出三部分的体积相加即得.
,然后分别求出三部分的体积相加即得.
(1)在菱形ABEF中,因为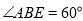 ,所以
,所以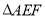 是等边三角形,又因为H是线段EF的中点,所以
是等边三角形,又因为H是线段EF的中点,所以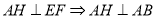
因为面ABEF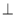 面ABCD,且面ABEF
面ABCD,且面ABEF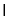 面ABCD=AB,
面ABCD=AB,
所以AH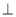 面ABCD,所以
面ABCD,所以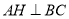
在直角梯形中,AB=2AD=2CD=4,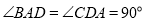 ,得到
,得到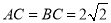 ,从而
,从而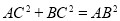 ,所以
,所以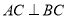 ,又AH
,又AH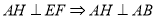 AC=A
AC=A
所以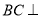 面AHC,又
面AHC,又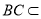 面BCE,所以平面AHC
面BCE,所以平面AHC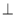 平面BCE .6分
平面BCE .6分
(2)因为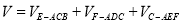 ,
,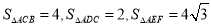
所以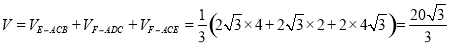 .12分
.12分
考点:(1)空间直线与平面的关系;(2)几何体的体积.


 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2013-2014学年四川省高三第六期3月阶段性考试文科数学试卷(解析版) 题型:选择题
已知一个三棱锥的主视图与俯视图如图所示,则该三棱锥的侧视图面积为( )
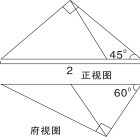
A.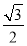 B.
B.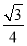 C.
C.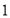 D.
D.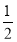
查看答案和解析>>
科目:高中数学 来源:2013-2014学年四川省高三二诊模拟文科数学试卷(解析版) 题型:选择题
已知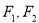 是椭圆的两个焦点,过
是椭圆的两个焦点,过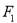 且与椭圆长轴垂直的直线交椭圆于A、B两点,若
且与椭圆长轴垂直的直线交椭圆于A、B两点,若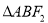 是正三角形,则这个椭圆的离心率是( )
是正三角形,则这个椭圆的离心率是( )
A.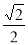 B.
B.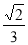 C.
C.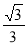 D.
D.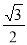
查看答案和解析>>
科目:高中数学 来源:2013-2014学年四川省高三三诊模拟理科数学试卷(解析版) 题型:选择题
已知椭圆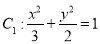 的左右焦点为
的左右焦点为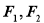 ,直线
,直线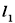 过点
过点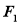 且垂直于椭圆的长轴,动直线
且垂直于椭圆的长轴,动直线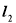 垂直于直线
垂直于直线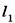 于点P,线段
于点P,线段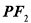 的垂直平分线与
的垂直平分线与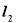 的交点的轨迹为曲线
的交点的轨迹为曲线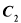 ,若
,若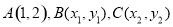 是
是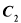 上不同的点,且
上不同的点,且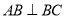 ,则
,则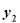 的取值范围是( )
的取值范围是( )
A.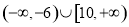 B.
B.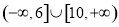
C.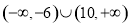 D.以上都不正确
D.以上都不正确
查看答案和解析>>
科目:高中数学 来源:2013-2014学年四川省高三三诊模拟文科数学试卷(解析版) 题型:填空题
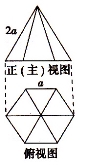
一个几何体的主视图和俯视图如图所示,主视图是边长为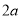 的正三角形,俯视图是边长为
的正三角形,俯视图是边长为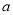 的正六边形,则该几何体左视图的面积是
的正六边形,则该几何体左视图的面积是
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com