
【题目】如图所示,∠PAQ是村里一个小湖的一角,其中∠PAQ=60°.为了给村民营造丰富的休闲环境,村委会决定在直线湖岸AP与AQ上分别建观光长廊AB与AC,其中AB是宽长廊,造价是800元/米;AC是窄长廊,造价是400元/米;两段长廊的总造价预算为12万元(恰好都用完);同时,在线段BC上靠近点B的三等分点D处建一个表演舞台,并建水上通道AD(表演舞台的大小忽略不计),水上通道的造价是600元/米. 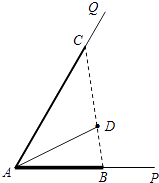
(1)若规划宽长廊AB与窄长廊AC的长度相等,则水上通道AD的总造价需多少万元?
(2)如何设计才能使得水上通道AD的总造价最低?最低总造价是多少万元?
【答案】
(1)解:设AB=AC=x(单位:百米),
则宽长廊造价为8x万元,窄长廊造价为4x万元,
故两段长廊的总造价为12x万元,所以12x=12,得x=1,
又∠PAQ=60°,△ABC是边长为1的正三角形,
又点D为线段BC上靠近点B的三等分点,所以BD= ![]() ,
,
在△ABD中,由余弦定理得
AD2=BA2+BD2﹣2BABDcos∠ABD=1+ ![]() ﹣2×
﹣2× ![]() ×
× ![]() =
= ![]() ,即AD=
,即AD= ![]() .
.
又水上通道的造价是6万元/百米,所以水上通道的总造价为2 ![]() 万元
万元
(2)解:设AB=x,AC=y(单位:百米),则两段长廊的总造价为8x+4y=12,
即2x+y=3,在△ABC中,由余弦定理得:
BC2=AB2+AC2﹣2ABACcos∠BAC=x2+y2﹣2xy ![]() =x2+y2﹣xy,
=x2+y2﹣xy,
在△ABC与△ABD中,由余弦定理及cos∠ABC=cos∠ABD,得
![]() =
= ![]() ,又BC=3BD,
,又BC=3BD,
得AD2= ![]() x2+
x2+ ![]() y2+
y2+ ![]() xy=
xy= ![]() x2+
x2+ ![]() (3﹣2x)2+
(3﹣2x)2+ ![]() x(3﹣2x)=
x(3﹣2x)= ![]() x2﹣
x2﹣ ![]() x+1
x+1
= ![]() (x﹣
(x﹣ ![]() )2+
)2+ ![]() ,当且仅当x=
,当且仅当x= ![]() 时,AD有最小值
时,AD有最小值 ![]() ,
,
故总造价有最小值3 ![]() 万元,此时y=
万元,此时y= ![]() ,
,
即当宽长廊AB为 ![]() 百米(75米)、窄长廊AC为
百米(75米)、窄长廊AC为 ![]() 百米(150米)时,
百米(150米)时,
水上通道AD有最低总造价为3 ![]() 万元.
万元.
【解析】【(1)设AB=AC=x(单位:百米),由题意可得12x=12,即x=1,求得BD= ![]() ,在△ABD中,由余弦定理求得AD的长,即可得到所求造价;(2)设AB=x,AC=y(单位:百米),则两段长廊的总造价为8x+4y=12,即2x+y=3,y=3﹣2x,运用余弦定理求得BC,再在△ABC与△ABD中,由余弦定理及cos∠ABC=cos∠ABD,求得AD2的解析式,化简整理,运用配方,即可得到所求最小值,及x,y的值.
,在△ABD中,由余弦定理求得AD的长,即可得到所求造价;(2)设AB=x,AC=y(单位:百米),则两段长廊的总造价为8x+4y=12,即2x+y=3,y=3﹣2x,运用余弦定理求得BC,再在△ABC与△ABD中,由余弦定理及cos∠ABC=cos∠ABD,求得AD2的解析式,化简整理,运用配方,即可得到所求最小值,及x,y的值.
【考点精析】解答此题的关键在于理解基本不等式在最值问题中的应用的相关知识,掌握用基本不等式求最值时(积定和最小,和定积最大),要注意满足三个条件“一正、二定、三相等”.


科目:高中数学 来源: 题型:
【题目】学校为测评班级学生对任课教师的满意度,采用“100分制”打分的方式来计分.现从某班学生中随机抽取10名,以下茎叶图记录了他们对某教师的满意度分数(以十位数字为茎,个位数字为叶):
规定若满意度不低于98分,测评价该教师为“优秀”.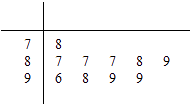
(1)求从这10人中随机选取3人,至多有1人评价该教师是“优秀”的概率;
记ξ表示抽到评价该教师为“优秀”的人数,求ξ的分布列及数学期望.
(2)以这10人的样本数据来估计整个班级的总体数据,若从该班任选3人,
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=Asin(ωx+)(A,ω,为常数,且A>0,ω>0,0<<π)的部分图象如图所示. 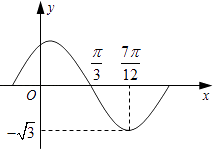
(1)求A,ω,的值;
(2)当x∈[0, ![]() ]时,求f(x)的取值范围.
]时,求f(x)的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=ln(1+x),g(x)=xf′(x),x≥0,其中f′(x)是f(x)的导函数.
(1)若f(x)≥ag(x)恒成立,求实数a的取值范围;
(2)设n∈N* , 证明: ![]() +
+ ![]() +…+
+…+ ![]() <ln(n+1).
<ln(n+1).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com