
【题目】在![]() 中,角
中,角![]() 、
、![]() 、
、![]() 所对的边分别为
所对的边分别为![]() 、
、![]() 、
、![]() ,
,![]() ,当角
,当角![]() 取最大值时,
取最大值时,![]() 的周长为
的周长为![]() ,则
,则![]() __________.
__________.
【答案】3
【解析】分析:根据题意由正弦定理得出cosA<0,A为钝角,cosAcosC≠0,由两角和的正弦函数公式,同角三角函数基本关系式可得出tanA=﹣3tanC,且tanC>0;由已知及基本不等式求出B取得最大值,可得C=B=![]() ,可求A,利用余弦定理可求a=
,可求A,利用余弦定理可求a=![]() b,结合已知求得b的值,进而可求a的值.
b,结合已知求得b的值,进而可求a的值.
详解:△ABC中,![]() sinB=cos(B+C)sinC,
sinB=cos(B+C)sinC,
∴![]() b=cos(B+C)c,即cosA=﹣
b=cos(B+C)c,即cosA=﹣![]() <0,∴A为钝角,
<0,∴A为钝角,
∴cosAcosC≠0;
由sinB=sin(A+C)=sinAcosC+cosAsinC=﹣2cosAsinC,
可得tanA=﹣3tanC,且tanC>0,
![]()
=![]()
当且仅当tanC=![]() 时取等号;
时取等号;
∴B取得最大值时,c=b=1,此时C=B=![]() .
.
∴A=![]() ,由a2=b2+c2﹣2bccosA,可得:a=
,由a2=b2+c2﹣2bccosA,可得:a=![]() b,
b,
∵三角形的周长为a+b+c=![]() b +b+b=2
b +b+b=2![]() .解得:b=
.解得:b=![]() ,可得:a=
,可得:a=![]() b =3.
b =3.
故答案为:3


科目:高中数学 来源: 题型:
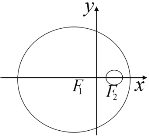
【题目】如图,已知圆![]() 的方程为
的方程为![]() ,圆
,圆![]() 的方程为
的方程为![]() ,若动圆
,若动圆![]() 与圆
与圆![]() 内切,与圆
内切,与圆![]() 外切.
外切.
(Ⅰ)求动圆圆心![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)过直线![]() 上的点
上的点![]() 作圆
作圆![]() 的两条切线,设切点分别是
的两条切线,设切点分别是![]() ,
,![]() ,若直线
,若直线![]() 与轨迹
与轨迹![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
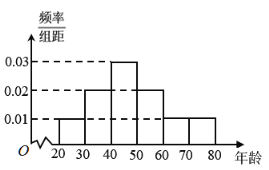
【题目】退休年龄延迟是平均预期寿命延长和人口老龄化背景下的一种趋势.某机构为了了解某城市市民的年龄构成,从该城市市民中随机抽取年龄段在[20,80]内的600人进行调查,并按年龄层次绘制频率分布直方图,如图所示.若规定年龄分布在[60,80]内的人为“老年人”,将上述人口分布的频率视为该城市年龄段在[20,80]的人口分布的概率.从该城市年龄段在[20,80]内的市民中随机抽取3人,记抽到“老年人”的人数为![]() 则随机变量
则随机变量![]() 的数学期望为______.
的数学期望为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若![]() 在
在![]() 处的切线方程为
处的切线方程为![]() ,求实数
,求实数![]() 、
、![]() 的值;
的值;
(2)设函数![]() ,
,![]() (其中
(其中![]() 为自然对数的底数).
为自然对数的底数).
①当![]() 时,求
时,求![]() 的最大值;
的最大值;
②若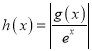 是单调递减函数,求实数
是单调递减函数,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场举行促销活动,有两个摸奖箱,![]() 箱内有一个“
箱内有一个“![]() ”号球,两个“
”号球,两个“![]() ”号球,三个“
”号球,三个“![]() ”号球、四个无号球,
”号球、四个无号球,![]() 箱内有五个“
箱内有五个“![]() ”号球,五个“
”号球,五个“![]() ”号球,每次摸奖后放回,每位顾客消费额满
”号球,每次摸奖后放回,每位顾客消费额满![]() 元有一次
元有一次![]() 箱内摸奖机会,消费额满
箱内摸奖机会,消费额满![]() 元有一次
元有一次![]() 箱内摸奖机会,摸得有数字的球则中奖,“
箱内摸奖机会,摸得有数字的球则中奖,“![]() ”号球奖
”号球奖![]() 元,“
元,“![]() ”号球奖
”号球奖![]() 元,“
元,“![]() ”号球奖
”号球奖![]() 元,摸得无号球则没有奖金。
元,摸得无号球则没有奖金。
(1)经统计,顾客消费额![]() 服从正态分布
服从正态分布![]() ,某天有
,某天有![]() 位顾客,请估计消费额
位顾客,请估计消费额![]() (单位:元)在区间
(单位:元)在区间![]() 内并中奖的人数.(结果四舍五入取整数)
内并中奖的人数.(结果四舍五入取整数)
附:若![]() ,则
,则![]() ,
,![]() .
.
(2)某三位顾客各有一次![]() 箱内摸奖机会,求其中中奖人数
箱内摸奖机会,求其中中奖人数![]() 的分布列.
的分布列.
(3)某顾客消费额为![]() 元,有两种摸奖方法,
元,有两种摸奖方法,
方法一:三次![]() 箱内摸奖机会;
箱内摸奖机会;
方法二:一次![]() 箱内摸奖机会.
箱内摸奖机会.
请问:这位顾客选哪一种方法所得奖金的期望值较大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一家商场销售一种商品,该商品一天的需求量在![]() 范围内等可能取值,该商品的进货量也在
范围内等可能取值,该商品的进货量也在![]() 范围内取值(每天进货1次).这家商场每销售一件该商品可获利60元;若供不应求,可从其他商店调拨,销售一件该商品可获利40元;若供大于求,剩余的每处理一件该商品亏损20元.设该商品每天的需求量为
范围内取值(每天进货1次).这家商场每销售一件该商品可获利60元;若供不应求,可从其他商店调拨,销售一件该商品可获利40元;若供大于求,剩余的每处理一件该商品亏损20元.设该商品每天的需求量为![]() ,每天的进货量为
,每天的进货量为![]() 件,该商场销售该商品的日利润为
件,该商场销售该商品的日利润为![]() 元.
元.
(1)写出这家商场销售该商品的日利润为![]() 关于需求量
关于需求量![]() 的函数表达式;
的函数表达式;
(2)写出供大于求,销售![]() 件商品时,日利润
件商品时,日利润![]() 的分布列;
的分布列;
(3)当进货量![]() 多大时,该商场销售该商品的日利润的期望值最大?并求出日利润的期望值的最大值.
多大时,该商场销售该商品的日利润的期望值最大?并求出日利润的期望值的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com