
【题目】某水果批发商经销某种水果(以下简称A水果),购入价为300元/袋,并以360元/袋的价格售出,若前8小时内所购进的A水果没有售完,则批发商将没售完的A水果以220元/袋的价格低价处理完毕(根据经验,2小时内完全能够把A水果低价处理完,且当天不再购进).该水果批发商根据往年的销量,统计了100天A水果在每天的前8小时内的销售量,制成如下频数分布条形图.
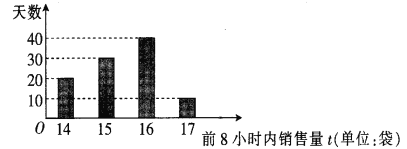
现以记录的100天的A水果在每天的前8小时内的销售量的频率作为A水果在一天的前8小时内的销售量的概率,记X表示A水果一天前8小时内的销售量,n表示水果批发商一天批发A水果的袋数.
(1)求X的分布列;
(2)以日利润的期望值为决策依据,在![]() 与
与![]() 中选其一,应选用哪个?
中选其一,应选用哪个?
【答案】(1)分布列见解析(2)选![]() .
.
【解析】
(1)由题意知,根据条形图,得到销售量分别为14,15,16,17的频率,进而得到随机变量X的分布列;
(2)分别求得当![]() 和
和![]() 时,利润的数学期望
时,利润的数学期望![]() ,比较即可得到结论.
,比较即可得到结论.
(1)由题意知,根据条形图,可得A水果在每天的前8小时内的销售量分别为14,15,16,17的频率分别是0.2,0.3,0.4和0.1 ,
所以X的分布列为
| 14 | 15 | 16 | 17 |
| 0.2 | 0.3 | 0.4 | 0.1 |
(2)当![]() 时,设Y为水果批发商的日利润,则Y的可能取值为760,900,
时,设Y为水果批发商的日利润,则Y的可能取值为760,900,
可得![]() ,
,
所以期望![]() ,
,
当![]() 时,设Z为水果批发商的日利润,则Z的可能取值为680,820,960,
时,设Z为水果批发商的日利润,则Z的可能取值为680,820,960,
可得![]() ,
,
所以期望![]() .
.
因为![]() ,
,
综上可知,当![]() 时的日利润期望值大于
时的日利润期望值大于![]() 时的日利润期望值,故选
时的日利润期望值,故选![]() .
.


科目:高中数学 来源: 题型:
【题目】下图是某市3月1日至14日的空气质量指数趋势图,空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染,某人随机选择3月1日至3月13日中的某一天到达该市,并停留2天.
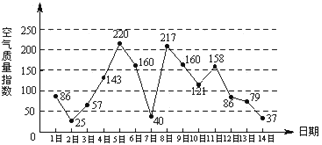
(Ⅰ)求此人到达当日空气重度污染的概率;
(Ⅱ)设X是此人停留期间空气质量优良的天数,求X的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市《城市总体规划(![]() 年)》提出到2035年实现“15分钟社区生活圈”全覆盖的目标,从教育与文化、医疗与养老、交通与购物、休闲与健身4个方面构建“15分钟社区生活圈“指标体系,并依据“15分钟社区生活圈”指数高低将小区划分为:优质小区(指数为
年)》提出到2035年实现“15分钟社区生活圈”全覆盖的目标,从教育与文化、医疗与养老、交通与购物、休闲与健身4个方面构建“15分钟社区生活圈“指标体系,并依据“15分钟社区生活圈”指数高低将小区划分为:优质小区(指数为![]() 、良好小区(指数为0.4-0.63、中等小区(指数为0.2~0.4)以及待改进小区(指数为0-0.2)4个等级.下面是三个小区4个方面指标值的调查数据:
、良好小区(指数为0.4-0.63、中等小区(指数为0.2~0.4)以及待改进小区(指数为0-0.2)4个等级.下面是三个小区4个方面指标值的调查数据:
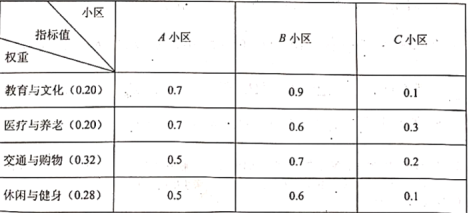
注:每个小区”15分钟社区生活圈”指数![]() 其中
其中![]() 、
、![]() 、
、![]() 、
、![]() 为该小区四个方面的权重,
为该小区四个方面的权重,![]() 为该小区四个方面的指标值(小区每一个方面的指标值为
为该小区四个方面的指标值(小区每一个方面的指标值为![]() 之间的一个数值)
之间的一个数值)
现有100个小区的“15分钟社区生活圈“指数数据,整理得到如下频数分布表:

(1)分别判断A、B、C三个小区是否是优质小区,并说明理由;
(2)对这100个小区按照优质小区、良好小区、中等小区和待改进小区进行分层抽样,抽取10个小区进行调查,若在抽取的10个小区中再随机地选取2个小区做深入调查,记这2个小区中为优质小区的个数为ζ,求ζ的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 在椭圆
在椭圆![]() :
: ![]() 上,
上, ![]() 是椭圆的一个焦点.
是椭圆的一个焦点.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)椭圆C上不与![]() 点重合的两点
点重合的两点![]() ,
, ![]() 关于原点O对称,直线
关于原点O对称,直线![]() ,
, ![]() 分别交
分别交![]() 轴于
轴于![]() ,
, ![]() 两点.求证:以
两点.求证:以![]() 为直径的圆被直线
为直径的圆被直线![]() 截得的弦长是定值.
截得的弦长是定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某省确定从2021年开始,高考采用“![]() ”的模式,取消文理分科,即“3”包括语文、数学、外语,为必考科目;“1”表示从物理、历史中任选一门;“2”则是从生物、化学、地理、政治中选择两门,共计六门考试科目.某高中从高一年级2000名学生(其中女生900人)中,采用分层抽样的方法抽取
”的模式,取消文理分科,即“3”包括语文、数学、外语,为必考科目;“1”表示从物理、历史中任选一门;“2”则是从生物、化学、地理、政治中选择两门,共计六门考试科目.某高中从高一年级2000名学生(其中女生900人)中,采用分层抽样的方法抽取![]() 名学生进行调查.
名学生进行调查.
(1)已知抽取的![]() 名学生中含男生110人,求
名学生中含男生110人,求![]() 的值及抽取到的女生人数;
的值及抽取到的女生人数;
(2)学校计划在高二上学期开设选修中的“物理”和“历史”两个科目,为了了解学生对这两个科目的选课情况,对在(1)的条件下抽取到的![]() 名学生进行问卷调杳(假定每名学生在这两个科目中必须洗择一个科目且只能选择一个科目).下表是根据调查结果得到的
名学生进行问卷调杳(假定每名学生在这两个科目中必须洗择一个科目且只能选择一个科目).下表是根据调查结果得到的![]() 列联表,请将列联表补充完整,并判断是否有
列联表,请将列联表补充完整,并判断是否有![]() 的把握认为选择科目与性别有关?说明你的理由;
的把握认为选择科目与性别有关?说明你的理由;
性别 | 选择物理 | 选择历史 | 总计 |
男生 | 50 | ||
女生 | 30 | ||
总计 |
(3)在(2)的条件下,从抽取的选择“物理”的学生中按分层抽样抽取6人,再从这6名学生中抽取2人,对“物理”的选课意向作深入了解,求2人中至少有1名女生的概率.
附: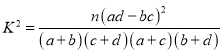 ,其中
,其中![]() .
.
| 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】万众瞩目的第14届全国冬季运动运会(简称“十四冬”)于2020年2月16日在呼伦贝尔市盛大开幕,期间正值我市学校放寒假,寒假结束后,某校工会对全校100名教职工在“十四冬”期间每天收看比赛转播的时间作了一次调查,得到如图频数分布直方图:
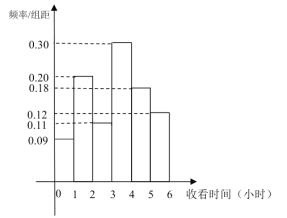
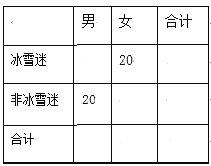
(1)若将每天收看比赛转播时间不低于3小时的教职工定义为“冰雪迷”,否则定义为“非冰雪迷”,请根据频率分布直方图补全![]() 列联表;并判断能否有
列联表;并判断能否有![]() 的把握认为该校教职工是否为“冰雪迷”与“性别”有关;
的把握认为该校教职工是否为“冰雪迷”与“性别”有关;
(2)在全校“冰雪迷”中按性别分层抽样抽取6名,再从这6名“冰雪迷”中选取2名作冰雪运动知识讲座.记其中女职工的人数为![]() ,求的
,求的![]() 分布列与数学期望.
分布列与数学期望.
附表及公式:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
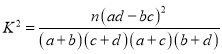 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为坐标原点,
为坐标原点,![]() 为坐标平面内动点,且
为坐标平面内动点,且![]() 成等差数列.
成等差数列.
(1)求动点![]() 的轨迹方程;
的轨迹方程;
(2)设点![]() 的轨迹为曲线
的轨迹为曲线![]() ,过点
,过点![]() 作直线交
作直线交![]() 于
于![]() 两点(不与原点重合),是否存在
两点(不与原点重合),是否存在![]() 轴上一定点
轴上一定点![]() ,使得_________.若存在,求出定点
,使得_________.若存在,求出定点![]() ,若不存在,说明理由.从“①作
,若不存在,说明理由.从“①作![]() 点关于
点关于![]() 轴的对称点
轴的对称点![]() ,则
,则![]() 三点共线;②
三点共线;②![]() ”这两个条件中选一个,补充在上面的问题中并作答(注:如果选择两个条件分别作答,按第一个解答计分)
”这两个条件中选一个,补充在上面的问题中并作答(注:如果选择两个条件分别作答,按第一个解答计分)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com