
(1)B′为B关于x轴的对称点(B′与A不重合),当![]() ·
·![]() =-1时,判断直线AB′是否恒过定点.
=-1时,判断直线AB′是否恒过定点.
(2)当直线AB恒过定点(m,0)(m>0,且m≠2)时,求∠AOB的取值范围.
解:(1)设A(x1,y1),B(x2,y2),则![]() ·
·![]() =x1x2+y1y2=-1.
=x1x2+y1y2=-1.
∵y12=2x1,y22=2x2,∴(y1y2)2=4x1x2.
∴![]() +y1y2=-1.∴y1y2=-2.
+y1y2=-1.∴y1y2=-2.
∵B′(x2,-y2),kAB′=![]() =
=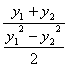 =
=![]() ,
,
AB′:y-y1=![]() (x-x1),即(y1-y2)y-y12+y1y2=2x-2x1,
(x-x1),即(y1-y2)y-y12+y1y2=2x-2x1,
由y12=2x1得(y1-y2)y=2x-y1y2=2(x+1),
∴直线AB′恒过定点(-1,0).
(2)kOA=![]() =
=![]() ,kOB=
,kOB=![]() ,不妨设y1>0,y2<0,
,不妨设y1>0,y2<0,
则∠AOB为OB到OA的角,
∴tan∠AOB=![]() =
=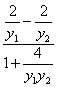 =
=![]() .
.
设直线AB方程为x=ay+m,代入y2=2x得y2-2ay-2m=0,则y1y2=-2m.
∴tan∠AOB=![]() (y1+
(y1+![]() ).
).
当m>2时,y1+![]() ≥2
≥2![]() ,∴tan∠AOB≥
,∴tan∠AOB≥![]() .∴arctan
.∴arctan![]() ≤∠AOB<
≤∠AOB<![]() .10分
.10分
当0<m<2时,tan∠AOB≤![]() ,
,
∴![]() <∠AOB≤π+arctan
<∠AOB≤π+arctan![]() .
.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:高中数学 来源: 题型:
(A)4 (B)8
(C)16 (D)32
查看答案和解析>>
科目:高中数学 来源: 题型:
已知抛物线C:y2=4x.
(1)若椭圆左焦点及相应的准线与抛物线C的焦点F及准线l分别重合,试求椭圆短轴端点B与焦点F连线中点P的轨迹方程;
(2)若M(m,0)是x轴上的一定点,Q是(1)所求轨迹上任一点,试问|MQ|有无最小值?若有,求出其值;若没有,说明理由.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年人教版高考数学文科二轮专题复习提分训练16练习卷(解析版) 题型:解答题
已知抛物线C:y2=2px(p>0)过点A(1,-2).
(1)求抛物线C的方程,并求其准线方程.
(2)是否存在平行于OA(O为坐标原点)的直线l,使得直线l与抛物线C有公共点,且直线OA与l的距离等于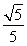 ?若存在,求出直线l的方程;若不存在,说明理由.
?若存在,求出直线l的方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年人教版高考数学文科二轮专题复习提分训练16练习卷(解析版) 题型:填空题
已知抛物线C:y2=2px(p>0)的准线为l,过M(1,0)且斜率为 的直线与l相交于点A,与C的一个交点为B,若
的直线与l相交于点A,与C的一个交点为B,若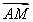 =
=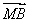 ,则p= .
,则p= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com