
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
| 2 |


科目:高中数学 来源: 题型:
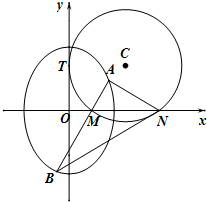 如图,圆C与y轴相切于点T(0,2),与x轴正半轴相交于两点M,N(点M在点N的左侧),且|MN|=3.
如图,圆C与y轴相切于点T(0,2),与x轴正半轴相交于两点M,N(点M在点N的左侧),且|MN|=3.| x2 |
| 4 |
| y2 |
| 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:
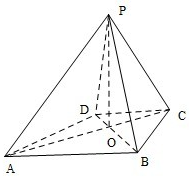 如图,已知四棱锥P-ABCD的底面ABCD为等腰梯形,AB∥DC,AC⊥BD,AC与BD相交于点O,且顶点P在底面上的射影恰为O点,又BO=2,PO=
如图,已知四棱锥P-ABCD的底面ABCD为等腰梯形,AB∥DC,AC⊥BD,AC与BD相交于点O,且顶点P在底面上的射影恰为O点,又BO=2,PO=| 2 |
| PM |
| PC |
查看答案和解析>>
科目:高中数学 来源: 题型:
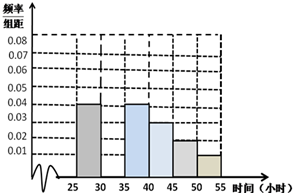 教育部,体育总局和共青团中央号召全国各级各类学校要广泛,深入地开展全国亿万大,中学生阳光体育运动,为此,某校学生会对高二年级2014年9月与10月这两个月内参加体育运动的情况进行统计,随机抽取了100名学生作为样本,得到这100名学生在该月参加体育运动总时间的小时数,根据此数据作出了如下的频数和频率的统计表和 频率分布直方图:
教育部,体育总局和共青团中央号召全国各级各类学校要广泛,深入地开展全国亿万大,中学生阳光体育运动,为此,某校学生会对高二年级2014年9月与10月这两个月内参加体育运动的情况进行统计,随机抽取了100名学生作为样本,得到这100名学生在该月参加体育运动总时间的小时数,根据此数据作出了如下的频数和频率的统计表和 频率分布直方图:| 分组 | 运动时间 (小时) | 频数 | 频率 |
| 1 | [25,30) | 20 | 0.2 |
| 2 | [30,35) | a | p |
| 3 | [35,40) | 20 | 0.2 |
| 4 | [40,45) | 15 | 0.15 |
| 5 | [45,50) | 10 | 0.10 |
| 6 | [50,55] | 5 | 0.05 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
| BA |
| BC |
| 3 |
| 2 |
| BC |
| BA |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
| A、[0,1) |
| B、[1,4] |
| C、[1,6] |
| D、[0,1]∪[3,8] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com