
已知函数f(x)=xln x,g(x)=x3+ax2-x+2.
(1)求函数f(x)的单调区间;
(2)对一切x∈(0,+∞),2f(x)≤g′(x)+2恒成立,求实数a的取值范围.
科目:高中数学 来源:2014年高考数学(理)二轮复习真题感悟常考问题9练习卷(解析版) 题型:填空题
若数列{an}的前n项和为Sn= an+
an+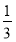 ,则数列{an}的通项公式是an=________.
,则数列{an}的通项公式是an=________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习真题感悟常考问题15练习卷(解析版) 题型:选择题
抛物线y2=4x的焦点到双曲线x2- =1的渐近线的距离是( ).
=1的渐近线的距离是( ).
A.  B.
B. C.1 D.
C.1 D. 
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习真题感悟x4-5练习卷(解析版) 题型:填空题
已知a,b,m,n均为正数,且a+b=1,mn=2,则(am+bn)(bm+an)的最小值为________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习真题感悟x4-4练习卷(解析版) 题型:填空题
如图,以过原点的直线的倾斜角θ为参数,则圆x2+y2-x=0的参数方程为______________.

查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习体系通关训练倒数第9天练习卷(解析版) 题型:选择题
函数f(x)的定义域为R,f(-1)=2,对任意x∈R,f′(x)>2,则f(x)>2x+4的解集为( ).
A.(-1,1) B.(-1,+∞)
C.(-∞,-1) D.(-∞,+∞)
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习体系通关训练倒数第9天练习卷(解析版) 题型:选择题
已知定义在R上的奇函数f(x)和偶函数g(x)满足f(x)+g(x)=ax-a-x+2(a>0且a≠1),若g(2)=a,则f(2)=( ).
A.2 B.  C.
C.  D.a2
D.a2
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习体系通关训练倒数第8天练习卷(解析版) 题型:选择题
已知sin α= ,则cos (π-2α)=( ).
,则cos (π-2α)=( ).
A. B.-
B.- C.
C.  D.
D. 
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习体系通关训练倒数第5天练习卷(解析版) 题型:选择题
设F1,F2是双曲线x2- =1的两个焦点,P是双曲线上的一点,且|PF1|-|PF2|=2,3|PF1|=4|PF2|,则△PF1F2的面积等于( ).
=1的两个焦点,P是双曲线上的一点,且|PF1|-|PF2|=2,3|PF1|=4|PF2|,则△PF1F2的面积等于( ).
A.4 B.8
B.8
C.24 D.48
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com